I am a huge proponent of using context to drive motivation and understanding in math classes.  Students need to see that math is not a bunch of disjointed abstract ideas thrown together, but something that is cohesive, has meaning and value, and surrounds them every day.  Framing math material in this way helps students access the content, provides a hook for why we should study math, and, in my experience, gives them a reason to persevere in the face of challenges. Additionally, as students see the math that encompasses the world around them, they begin to understand that math can be used to model real-world scenarios.

Plenty of misconceptions surround Standard for Mathematical Practice (SMP) 4: Model with Mathematics.  For many, the misconceptions lie in the fact that they are looking to model “THE” mathematics.  They believe that by using manipulatives or showing students how to do something, they are modeling with mathematics.  In reality, they are modeling the mathematics with other tools.  This SMP calls for us to model “WITH” mathematics, meaning that we need to use mathematics to model the world around us.  Math educators need to facilitate these modeling opportunities for students. In order to do that, we need to understand what modeling with mathematics looks like and what we can and should expect to see in instructional materials to aid this endeavor.

In the non-examples above, you’ll see two common misconceptions about what modeling with mathematics looks like in instructional materials. These non-examples ask students to create models to reflect the mathematics in the two problems, while items that properly reflect SMP 4, such as the example above, would ask students to apply math skills to solve a real-life scenario that has meaning for students.

Modeling with mathematics has common foundational elements that students will engage in at varying degrees depending on grade level.  For example, in later grades, tasks that require students to model with mathematics will involve some assumptions and these assumptions will help simplify the problem.  At the early elementary level students will be given all relevant information.

As we look toward middle school, students start making assumptions, as they would when using math in the real world, about different constraints present within the task.  In some cases students may be asked to find that information; in others, students could be given the information once they have identified that they need it.  In high school, tasks should require students to make multiple assumptions and students should be expected to find those values using various tools and resources, providing justification for the assumptions they made and values they picked.

In an early middle school example above, students need to identify pieces of information they would need to solve the problem.  That information, along with any other information they may need could then be provided to the students so that they could finish finding an estimate for the cost to tile the floor.  Additionally, you will notice that this problem can be approached in a variety of ways.  Some students might use the area formula to help determine the number of tiles they need while others might use an array or draw a diagram, while others might want manipulatives to help them build their floor.  In all of these cases, students are using the mathematics that they already know as they engage in the task and try to find a solution.

In the problem above, students would need to identify what information they’d need to know in order to be able to answer the questions. Depending on the grade level, students would be given, or would need to find, a tool for finding the inflation rate between two years and use the inflation rate to find the current value of 10 cents in 1938.

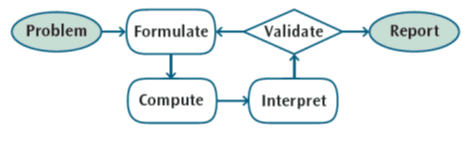
It is important to remember that modeling with mathematics is a process, not just presenting mathematical representations of a scenario.  Multiple variations of the following graphic have been used to aid in understanding that process.  The difference that will be occurring from grade band to grade band will be in how students are engaging in the cycle of formulating (developing a mathematical representation), computing (manipulating that representation to obtain the desired outcome), analyzing (interpreting the results and their meaning in relation to the original problem) and validating.  Elementary students will start by engaging in tasks that might only require them to go through that cycle once before they report their findings.  Middle school students should be engaged in tasks that will have them progress through the cycle a few times, while high school students should have tasks that requires them to repeatedly engage in that cycle.

As you may have noticed, it is impossible for students to engage in modeling with mathematics without engaging in other math practices.  At the very least, student should also be engaged in making sense of problems and persevering in solving them, reasoning abstractly and quantitatively, and attending to precision.  As tasks get more complex, students should also be engaged in constructing viable arguments and critiquing the reasoning of others, using appropriate tools strategically, and looking for and making use of structure.

In the Practicing Skills example above, students are given the opportunity to apply their knowledge to specific examples.  This provides isolated instances where students can intentionally engage in a specific skill or strategy to determine the result.  In the Engaging in Modeling with Mathematics example, students have the opportunity to use all of their mathematical understandings to try and find solutions.  While students could select concrete values and apply similar skills as they would in the other example, there is no intended strategy or method for finding the solution.

I tend to see these tasks as a method of assessing students’ mastery of different mathematical skills and concepts.  This is not to say that learning cannot occur when modeling with mathematics, but it is not the primary purpose of a modeling task.  Students should be utilizing the mathematics that they already know, not looking to develop new ideas or concepts.  As a result of engaging in a modeling task, it is possible for students to deepen their understandings of mathematics and see different ways that ideas can connect together.