When I was asked to continue the series of the Most Misunderstood Standards for grades 3–5, I immediately said yes! After all, the series is a perfect combination of my two most favorite things: math and writing! Over the course of my 18-year career as a teacher and instructional coach, I have had the privilege to learn deeply about the standards, the Shifts, and the mathematical practices from some of the best math educators in the country. With their guidance, I developed an understanding of what excellent math instruction is in an elementary school classroom.
As a math coach, I often plan with teachers and observe in their classrooms. We use the Instructional Practices Guide for Coaching as our North Star. You can learn more about the recently updated coaching tool here. During my time supporting and coaching teachers in classrooms, I have noticed that particular standards seem to be misunderstood or the instruction associated with a standard doesn’t meet the rigor called for by the standard. While I know this is unintentional, it is important for us to understand why the instruction is misaligned. I hope through this series of posts for grades 3–5, we can begin to recognize pedagogical moves that support students doing the math!
I would like to take a closer look at two of my favorite third grade standards, 3.NF.A.3 and 3.OA.B.5.
3.NF.A.3: Explain equivalence of fractions in special cases and compare fractions by reasoning about their size.
For as long as I can remember, fractions have been the thorn in elementary school teachers’ sides. After a professional learning opportunity, I often hear teachers discussing personal fraction stories. Statements like, “Well I never learned fractions that way” or, “If I had learned fractions the way we teach kids now maybe I would have done better in high school math” are common in hallways after educators dig into the standards at a conceptual level. As we begin to think about fraction conceptually, I want us to look at an Illustrative Mathematics task together.
Task
Jon and Charlie plan to run together. They are arguing about how far to run. Charlie says, I run 3/6 of a mile each day. Jon says, I can only run 1/2 of a mile. If Charlie runs 3/6 of a mile and Jon runs 1/2 of a mile, explain why it is silly for them to argue. Draw a model or a number line to support your reasoning.
What do we want students to know and be able to do as a result of working this task?
- We want students to draw a model to reason about the length each boy runs.
- We want them to consider which model is the best to use- even though the task names two ways. (Which representation is a better model for distance?)
- We want students to notice and wonder.
I notice 3/6 and ½ are the same size.
I notice they are on the same place on the number line.
I wonder what that means.
- We want them to use what they know about fractions in this problem to make a conjecture about fraction equivalence.
Examples of what we want students to say:
Equivalent fractions name the same place on the number line.
Equivalent fractions take up the same amount of space.
Misaligned instruction often includes more of a focus on 3.NF.A3C. In the case of Jon and Charlie, it is common to see an emphasis on students being able to say: Jon and Charlie shouldn’t be arguing. They ran the same amount.
They are absolutely correct in their answer; however, as a teacher we need to know more about what the student knows. The following questions will support our students’ understanding of equivalency:
How do you know they ran the same amount?
What do you notice about your models? What do you notice about your number lines?
Do you think this is true in all cases of fraction equivalency? Why or why not?
The next standard I would like us to discuss is 3.OA.B.5: Apply properties of operations as strategies to multiply and divide.
Let’s examine a multiplication equation: 4 x 7 = 28. If a student does not know 4 x 7 by memory, they will need a strategy to help them solve the problem. Behold the distributive property!
By decomposing the 7 into 5 and 2, most students can access the problem. If they don’t know 2s and 5s by memory, skip counting can be used as well. The distributive property serves as a strategy for solving multiplication problems and supports a deep understanding of the concept of multiplication.
No wonder the properties of multiplication are misunderstood and often disliked by students! They are sometimes asked to memorize a procedure before they understand the concept. For example, the distributive property formula a(b + c) = (a x b) + (a x c) is taught before their conceptual understanding is built. What if we taught the distributive property as a way to understand multiplication? I know many students would no longer say, “I always forget what to multiply and what to add.” The distributive property can be applied as a strategy for solving multiplication problems. Learning the strategy in third grade prepares students to multiply multi-digit numbers in fourth grade-a beautiful example of across grade-level coherence.
Teaching elementary school mathematics is certainly not elementary. At times, it can be challenging and quite complex. I hope my experiences as a third-grade teacher and an instructional coach provide you with support and clarity as you start the school year. Thank you for your commitment to excellent daily math instruction for all students. See you next month when we dive into Grade 4. I look forward to continuing this conversation. (You can find me on Twitter @few_rebecca.) Stay tuned and continue to #InstructUP!

















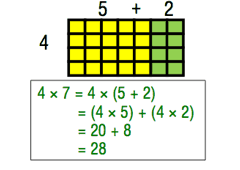


Do have an approximate time for the 4th grade misunderstood standards? I thought the third grade was very informative and am anxious to see the next set.
Thanks, Angie! Rebecca is working on grade 4 as we speak. I expect it will be posted within the next two weeks! Stay tuned!
https://apps.mathlearningcenter.org/partial-product-finder/
I recently came across this relevant virtual manipulative and I’m finding lots of teachers I know are unaware of it.
Thank you!
I love this! Thank you for sharing it.
Excellent tool for our current situation of teaching in a remote instructional setting. This visual supports development of multiplication facts, too! Thanks for sharing.
Thank you! Great information!
Thank you for the illustrations, common core connections and explaining this so well. Looking forward to the next issue.
Do you have an approximate date for the fifth grade standards?
I have used a highly visual method in the past: cut construction paper into strips about 1 1/2 inches wide. Label one strip with a “1”. This represents one whole. Fold another strip in half and cut on the fold. Label each piece “1/2”. Continuing like this can give you 1/3, 1/4, 1/6, 1/8 and even 1/12 if you desire. Students can then line them up vertically from largest strip to smallest strip and they will start to make connections. You can then do activities such as, “How many sixths does it take to make one third?” The visual of 2/4 being the same as 1/2 is very powerful. When you are done with the ones you can make 2/3 and 3/4 (even 5/6) and show how two of 1/3 make up 2/3. Etc etc. You can bring them out for several class periods and even play games with them. It may sound laborious but my principal was thrilled when she walked in unannounced for this activity. And it’s fun for the students too!
And for those that can’t find time to construct this fraction activity, search teacher pays teacher.
A good music class would make both of these concepts easy to understand.
3.NF.A1 Understanding fractions is such an important concept due to its carry over to all parts of the whole questions.
Hi.
Have you identified the most misunderstood standards in grades K-2?
Not yet, but we’re looking for an author and hope to publish those soon!
GREAT RESOURCE! We used this blog post in a district professional learning/collaboration session with all of our 3rd-grade math teachers. In the exit survey, ALL of the teachers rated the time spent reading and discussing as “VERY USEFUL”.
Oh that’s so great to hear. Thanks for sharing, Casey. Glad it was useful for the training!
Do you have a good 3rd/4th grade curriculum resource for math?
I signed up for the webinar, rushed home, and all I get is “on demand”. I’m confused!
The webinar began at 7 p.m. ET on 8/7/19. Is that when you tried to log in? If you were eligible for the on-demand version, it sounds like you joined at least an hour after the start–otherwise you would have entered the live webinar in progress. Rest assured the on-demand version is the same as the live version, apart from the ability to pose questions live to the authors.
Rebecca,
As I read your review of the 3rd grade most misunderstood standards, it occurred to me that much of the confusion exists because we include concepts and ideas that we actually only want students to be able to explore and gain insight and understandings about, and call them state standards.
1. If we call a concept or idea a “state standard,” the concept is tested on state assessments.
2. These assessment questions guide teachers and curriculum manufacturers in how they develop lessons on the concept and in what the final expectation should be on how a student shows proficiency on that specific standard. (Backwards Design)
Maybe there should be standards that are specifically measured in assessments using differing DOK questions, and a list of of grade specific explorations that are not assessed, but are included in all curriculum.