
-
- 09/08/13 | Adjusted: 08/01/18 | 1 file
- Grades 6
- 09/08/13 | Adjusted: 08/01/18 | 1 file
Cup of Rice
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: 6.NS.A.1, 5.NF.B.7, and MP.3
- Involves concepts, procedure, and application of fraction division – all required by standard 6.NS.A.1
- Devotes attention to a mathematically important case (dividend equal to 1)
- Builds on fraction division work from fifth grade (see 5.NF.B.7)
- Engages students in constructing viable arguments and critiquing the arguments of others (MP.3)
In the classroom:
- Uses visual models to support understanding
- Allows for individual or group work
- Encourages students to share their developing thinking
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to English Language Learner best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Elicits evidence of thinking both verbally and in written form.
- Includes a mathematical routine that reflects best practices for supporting English Language Learners in accessing mathematical concepts.
- Provides students with support in negotiating written word problems through multiple reads and/or multi-modal interactions with the problem.
-
Making the Shifts
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the major work of sixth grade Coherence Addresses the culminating standard in the progression of fraction operations; prepares for rational arithmetic in grade 7 Rigor Conceptual Understanding: primary in this task
Procedural Skill and Fluency: secondary in this task
Application: primary in this task -
Task
Tonya and Chrissy are trying to understand the following story problem for 1 ÷ $\frac{2}{3}$.
There is $\frac{2}{3}$ cup of rice in one serving of rice. I ate 1 cup of rice. How many servings of rice did I eat?
Tonya says, "One cup of rice contains $\frac{2}{3}$ cup serving plus an additional $\frac{1}{3}$ cup of rice, so the answer should be $1\frac{1}{3}$ servings."
Chrissy says, "I heard someone say that the answer is $\frac{3}{2}$ or $1\frac{1}{2}$ servings."
Is Tonya correct or incorrect? Explain your reasoning. Support your explanation using this diagram.
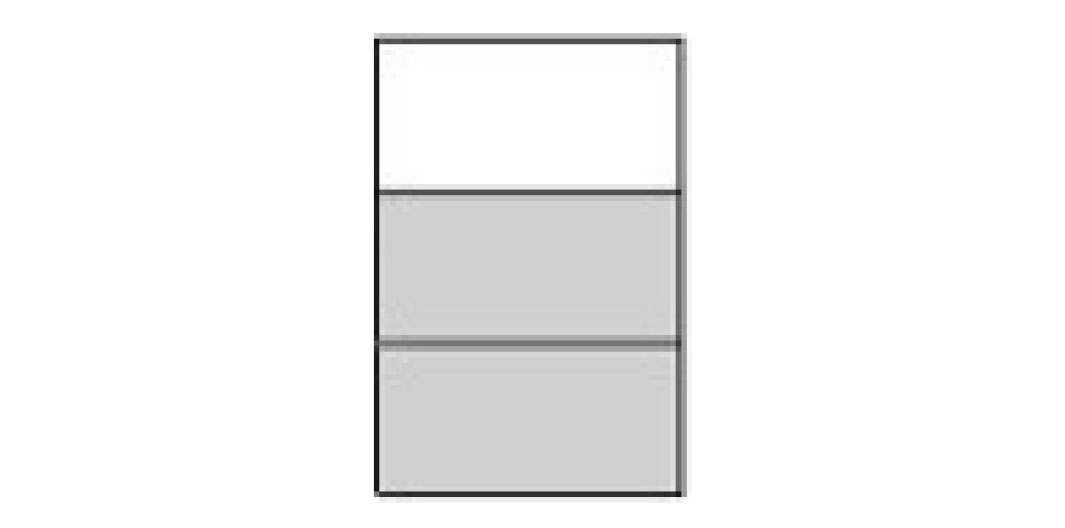
-
Illustrative Mathematics Commentary and Solution
Commentary:
One common mistake students make when dividing fractions using visuals is the confusion between remainder and the fractional part of a mixed number answer. In this problem, $\frac{1}{3}$ is the remainder with units "cups of rice" and $\frac{1}{2}$ has units "servings", which is what the problem is asking for.
Solution:
In Tonya's solution of $1\frac{1}{3}$, she correctly notices that there is one $\frac{2}{3}$-cup serving of rice in $1$ cup, and there is $\frac{1}{3}$cup of rice left over. But she is mixing up the quantities of servings and cups in her answer. The question becomes how many servings is $\frac{1}{3}$ cup of rice? The answer is "$\frac{1}{3}$ cup of rice is $\frac{1}{2}$ of a serving."

It would be correct to say, "There is one serving of rice with $\frac{1}{3}$ cup of rice left over," but to interpret the quotient $1\frac{1}{2}$, the units for the $1$ and the units for the $\frac{1}{2}$ must be the same:
There are $1\frac{1}{2}$ servings in $1$ cup of rice if each serving is $\frac{2}{3}$ cup.
-
Additional Thoughts
The quotient chosen for this problem, $1 ÷ \frac{2}{3} = \frac{3}{2}$, sheds light on the fact that dividing is multiplying by the reciprocal. Once students understand a quotient like $1 ÷ \frac{2}{3} = \frac{3}{2}$, they can think about a problem like $\frac{3}{4} ÷ \frac{2}{3}$ by taking $\frac{3}{4}$ of the known quotient $1 ÷ \frac{2}{3}$. That is, $\frac{3}{4} ÷ \frac{2}{3} = \frac{3}{4} × 1 ÷ \frac{2}{3} = \frac{3}{4} × \frac{3}{2}$.
For more insight into the expectations for fraction division, read pages 5 and 6 of the progression document, 6-8 The Number System.