
-
- 11/01/13 | Adjusted: 08/01/18 | 1 file
- Grades 7
- 11/01/13 | Adjusted: 08/01/18 | 1 file
Art Class, Assessment Variation
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: 7.RP.A.2 and MP.8
- Investigates several aspects of proportional relationships (equivalent ratios, unit rates, equations)
- Rewards the practice of looking for and expressing regularity in repeated reasoning (MP.8) in the table
In the classroom:
- Showcases a drop-down menu response method, but is easily replicated in the classroom as a fill-in-the-blank
- Provides an engaging application that could be tested in a lab-style setting
- Can lead into related discussions with the other tasks addressing 7.RP.A.2 in this set (Robot Races and Buying Bananas)
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Elicits evidence of student thinking both verbally and in written form
- Includes a mathematical routine that reflects best practices to supporting ELLs in accessing mathematical concepts.
- Provides students with support in negotiating written word problems through multiple reads and/or multi-modal interactions with the problem.
-
Making the Shifts
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the major work of seventh grade Coherence Expands on the idea of isolated ratios to developing the notion that ratios define proportional relationships; Builds on previous understandings of ratios to include ratios of rational numbers Rigor Conceptual Understanding: secondary in this task
Procedural Skill and Fluency: not targeted in this task
Application: primary in this task
-
Task
The students in Ms. Baca's art class were mixing yellow and blue paint. She told them that two mixtures will be the same shade of green if the blue and yellow paint are in the same ratio.
The table below shows the different mixtures of paint that the students made.
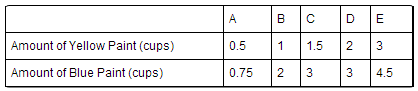
- How many different shades of paint did the students make?
- Which mixture(s) make the same shade as mixture A?
- How many cups of yellow paint would a student add to one cup of blue paint to make a mixture that is the same shade as mixture A?
- Let $b$ represent the number of cups of blue paint and $y$ represent the number of cups of yellow paint in a paint mixture. Write an equation that shows the relationship between the number of cups of yellow paint, $y$, and the number of cups of blue paint, $b$, in mixture E.
-
Illustrative Mathematics Commentary and Solution
Commentary:
This task is part of a joint project between Student Achievement Partners and Illustrative Mathematics to develop prototype machine-scorable assessment items that test a range of mathematical knowledge and skills described in the CCSSM and begin to signal the focus and coherence of the standards.
Task Purpose:
This task is part of a set of three assessment tasks for 7.RP.A.2.
7.RP.A.2 Art Class requires students to decide whether two quantities are in a proportional relationship by testing for equivalent ratios in a table, to find a unit rate for a ratio defined by non-whole numbers, and to represent a proportional relationship with an equation. Part (a) essentially asks students to partition a set of ratios displayed in a table into two sets of equivalent ratios. Part (b) asks students to identify all the ratios in the table that are equivalent to a given ratio. These two parts work together: the first question asks students to make a judgment about how many different proportional relationships are represented in the table, and the second asks students to specifically identify all of the ratios that go with one of those relationships. This task shows a shift in the standards that expand upon common approaches to "proportional reasoning” because it requires students to understand different aspects of proportional relationships, not just their ability to set up and solve a proportion.
Mathematical Content:
Students must work with ratios of whole numbers and common decimals between 0-5. Ratios involving only whole numbers were introduced in the prior grade; the 7th grade expectation is that students will work with ratios of non-whole numbers. Additionally, this task addresses the transition between working with ratios in isolation to thinking of ratios as defining proportional relationships.
Mathematical Practices:
The second task addresses several standards for mathematical practice. While it is possible that students have thought about what makes one paint mixture the same shade as another, it is unlikely they have thought about this from a mathematical perspective. Thus, students will need to make sense of the context and choose a mathematical approach to answer the questions given (there are multiple approaches). Most approaches require multiple steps, so students will need to make sense of the problem and persevere in solving it (MP.1). Students solving this task may look for structure (MP.7) by converting all five ratios into unit ratios and then grouping the ratios that have the same unit ratio. Students might also find equivalent ratios with the same amount of one kind of paint or the same total amount of paint. Any solution approach requires students to decontextualize and contextualize (MP.2). The complexity of the item could be lowered by asking Part (b), Part (c), and then Part (a) because it would suggest a solution approach to Part (a). Complexity could be increased by removing Part (c) which helps students choose a solution method for Part (d).
Solution:
- The students made $2$ different shades of paint.
- Mixtures D and E make the same shade as mixture A.
- A student should add $\frac{2}{3}$ cup of yellow paint to $1$ cup of blue paint to make the same shade as mixture A.
- Either of these equations would be correct:
- $b=\frac{3}{2}y$ (or $\frac{3}{2}y=b$ if this is a fill-in-the-blank)
- $y=\frac{2}{3}b$ (or $\frac{2}{3}b=y$ if this is a fill-in-the-blank)
-
Additional Thoughts
As noted in the Commentary above, this task is the second in a set of three tasks. The other tasks in the set can be found here: Robot Races and Buying Bananas. Robot Races asks students to "explain what a point ($x$, $y$) on the graph of a proportional relationship means in terms of the situation" and to "compute unit rates associated with ratios of fractions." Buying Bananas requires students to find a unit rate for a ratio of non-whole numbers.
For more information on proportional relationship expectations at grade seven, read pages 8–10 of the progression document, 6–7, Ratios and Proportional Relationships.
For more analysis on this task from an assessment perspective, read the Cognitive Complexity section on the Illustrative Mathematics site.