
-
- 06/05/14 | Adjusted: 08/01/18 | 1 file
- Grades K
- 06/05/14 | Adjusted: 08/01/18 | 1 file
Dice Addition 1
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: K.CC.A.3, K.OA.A.2
- Provides opportunities to practice addition fact fluency in a quick and efficient way for standards K.CC.A.3 and K.OA.A.2
- Connects ideas across domains: counting writing, and sequence of numbers (Counting and Cardinality) and addition (Operations and Algebraic Thinking)
- Encourages students to practice writing numbers while considering more complex mathematical topics
In the classroom:
- Provides opportunities and suggestions for meaningful differentiation
- Allows for partner work in which students can share addition strategies
- Offers an engaging activity that simultaneously targets students' procedural skill and conceptual understanding
- Can be used throughout the year to reinforce mathematical skills
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Includes a mathematical routine that reflects best practices to supporting ELLs in accessing mathematical concepts.
- Provides opportunities to support students in connecting mathematical language with mathematical representations.
-
Making the Shifts
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the major work of kindergarten Coherence Begins the development of addition facts that culminates with fluency in second grade (2.OA.B.2) Rigor Conceptual Understanding: secondary in this task
Procedural Skill and Fluency: primary in this task
Application: not targeted in this task
-
Task
Materials:
Each pair of students needs:
- One worksheet
- Two markers of different colors
- One pair of dice
Action:
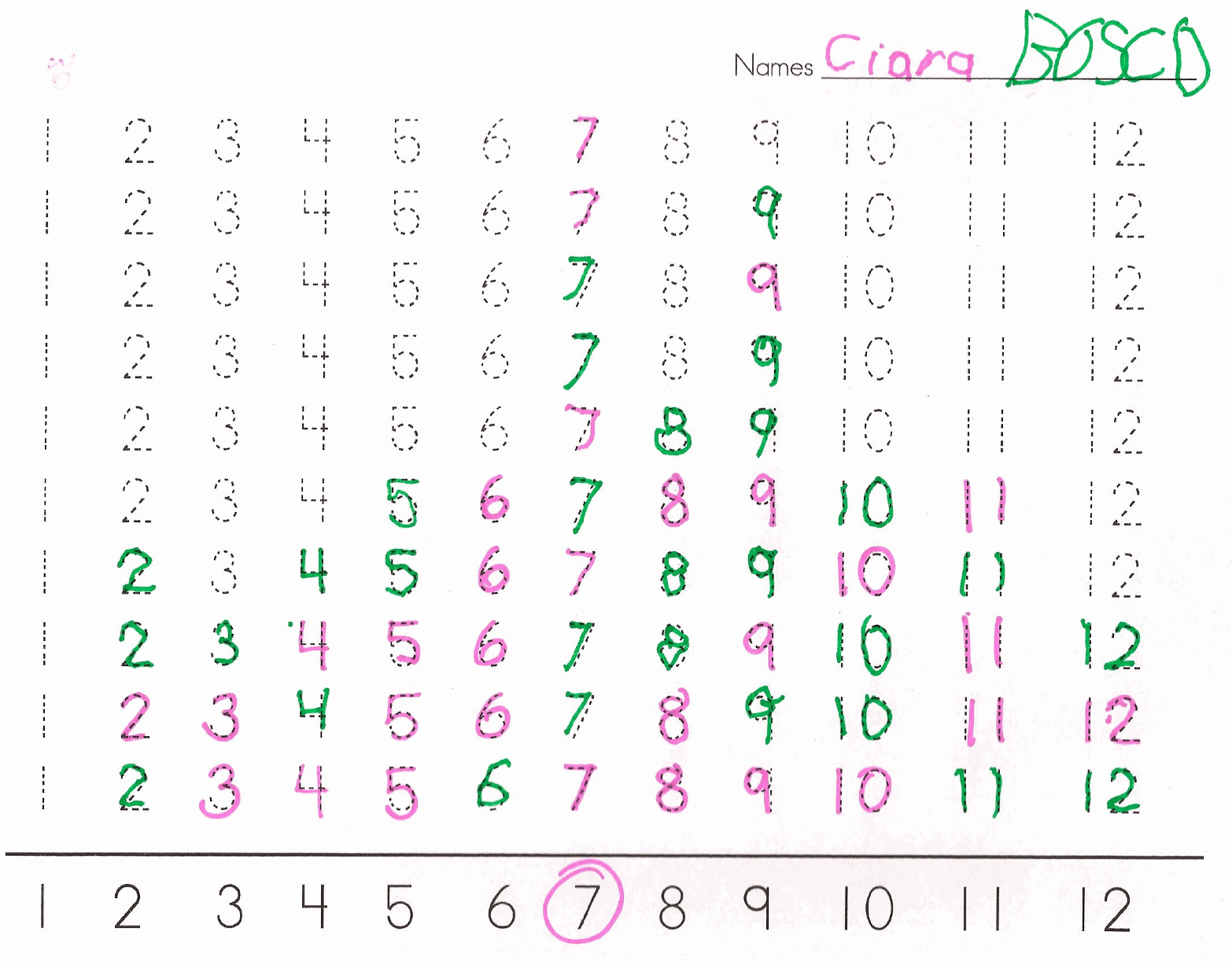
Student A rolls the two dice, finds the sum, and traces the number on the worksheet which corresponds to the answer with his/her marker. Student A then passes the dice to Student B who rolls both the dice, finds the sum, and traces the correct number on the worksheet with his/her marker. Play continues this way until one of the numbers "wins" (i.e., all of the numbers of that quantity have been traced).
-
Illustrative Mathematics Commentary and Solution
Commentary:
This task supports students in correctly writing numbers. Because students have to trace the number instead of coloring in a bubble with the number in it or circling the correct number, they gain handwriting practice as well as counting and addition practice.
The standard for kindergarten is addition to 10. This game uses two commercially available six-sided dice, and because of this students will practice addition to 12. If a teacher feels his/her class is not ready for addition to 12 they can use two spinners of 1-5 (or even 0-5) or use non-standard dice which go 0-5 or 1-5.
The teacher can start this game with dot dice so that students can count the dots to determine the sum. If the teacher would like to differentiate for students that need more of a challenge s/he can change the dice so that one die has written numbers and once die has dots. This will encourage students to practice counting on. The teacher could also give students two dice with written numbers. Teachers can strategically give different students different types of dice as a way of differentiating. This activity is an excellent independent center which students can play from the time they have been introduced to addition until the end of the school year.
As an extension, after students have played this game several times, the teacher can take a few completed game boards and the class can talk about trends they see and why. For example, no one ever gets the sum of one, why is that? Also if many games boards are compared students will probably find that numbers 6, 7, 8 and 9 win more often then numbers 2 and 12. The class could discuss this finding and why they believe it happens.
As an extension to this task see K.OA Dice Addition 2, which deals with the same concept but has students write out the equations they create with the dice.
Solution:
There is no one solution for this task. Students have correctly solved the task when they have taken turns, counted the dots on their dice, and recorded the sum until one number is the "winner."
-
Additional Thoughts
Students enter Kindergarten with a variety of mathematical understandings. This task can be easily adjusted to support that developing understanding simply by varying the type of dice that students are using. In all cases, students will have to use their understanding of addition as putting together.
Two dice with dots will give students a visual model that will allow them to count the total number of dots to find the sum. With time and practice, students come to quickly recognize the cardinalities of small groups without having to count the objects. This is called perceptual subitizing. As students work with this task using dice with dots, they develop their skill of conceptual subitizing – recognizing that a collection of objects is composed of two sub collections and quickly combining their cardinalities to find the cardinality of the collection.
Students progress from counting the total to being able to count forward, beginning from a given number within the known sequence (K.CC.A.2). The use of one die with numerals and another with dots will help facilitate this understanding and provide repeated practice with that skill. Experience with counting helps students to understand that the number of objects is the same regardless of their arrangement. This connection will continue in grade 1 with more advanced methods for counting-on, in which a counting word represents a group of objects that are added or subtracted and addends becomes embedded within the total (1.OA.C.6).
Using dice that both have numerals brings students from a concrete experience seeing and counting dots, to a more abstract one in which students demonstrate understanding of addition as combining values to find a sum. The variety of options for differentiation is beneficial to the wide range of student abilities found in a kindergarten classroom.
As an extension of this activity, teachers could ask their students what number combinations gave them different sums. (e.g., what different dice combinations did you roll to get the sum of 8? 6,2; 5,3; 4,4; 3,5; and 2,6) As the teacher writes an addition equation for each sum, students are seeing how to decompose numbers into pairs (K.OA.A.3). Students may offer other options that weren’t possible using the dice. This also may give students a first glance into the commutative property of addition.
This task develops students’ understanding of counting, cardinality, and addition. For more insight on the grade-level concepts addressed in this task, read pages 6–11 of the progression document, K Counting and Cardinality; K–5 Operations and Algebraic Thinking.