• Making the Shifts
• Task
• The purpose of this task is to provide students with a concrete situation they can model by dividing a whole number by a unit fraction. For students who are just beginning to think about the meaning of division by a unit fraction (or students who have never cooked), the teacher can bring in a 1/4 cup measuring cup so that students can act it out. If students can reason through parts (a) and (b) successfully, they will be well-situated to think about part (c) which could yield different solution methods.

  Commentary:

  The purpose of this task is to provide students with a concrete situation they can model by dividing a whole number by a unit fraction. For students who are just beginning to think about the meaning of division by a unit fraction (or students who have never cooked), the teacher can bring in a 1/4 cup measuring cup so that students can act it out. If students can reason through parts (a) and (b) successfully, they will be well-situated to think about part (c) which could yield different solution methods.

  Students may need a great deal of practice seeing the connection between the visual representation and the more abstract equations. This task provides an excellent opportunity for teachers to emphasize the relationship between multiplication and division, and if students do not automatically see the connection, the teacher should draw their attention to it.

  The approaches described in the solution can be used to make the connection between dividing by a whole number and multiplying by its reciprocal. If students are just beginning to understand the meaning of dividing by a unit fraction, such a conversation should be postponed. However, if they feel comfortable solving these kinds of problems with pictures, this task provides a perfect opportunity to see that dividing a whole number by a unit fraction is the same as multiplying by the reciprocal of the unit fraction. This, in turn, prepares them for the more general result that dividing by any fraction is the same as multiplying by its reciprocal, which students will see in 6th grade.

  Solution:

       a. Carolina needs 8 quarter cups of sour cream because there are 4 quarter cups in 1 cup, and so it takes $2×4=8$ quarter cups to make 2 cups:

  
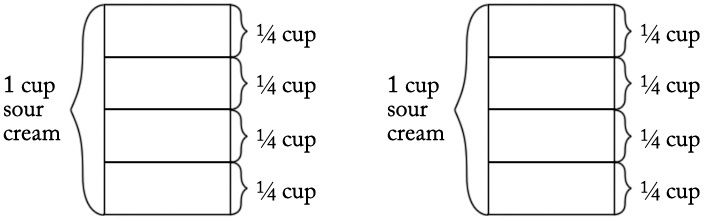
  This is a "how many groups?" division problem because it asks "How many quarter cups are in 2 cups?"
  There are two correct equations:

  $2÷\frac{1}{4}=?$

  
  or equivalently:

  $?×\frac{1}{4}=2$

  
  We can verify that 8 is the correct solution by noting that $8×\frac{1}{4}=\frac{8}{4}=2$ (4.NF.B.4c)

       b. Carolina needs 16 quarter cups of milk because there are 4 quareter cups in 1 cup and so $4×4$ quarter cups in 4 cups, as we see in this picture:
  
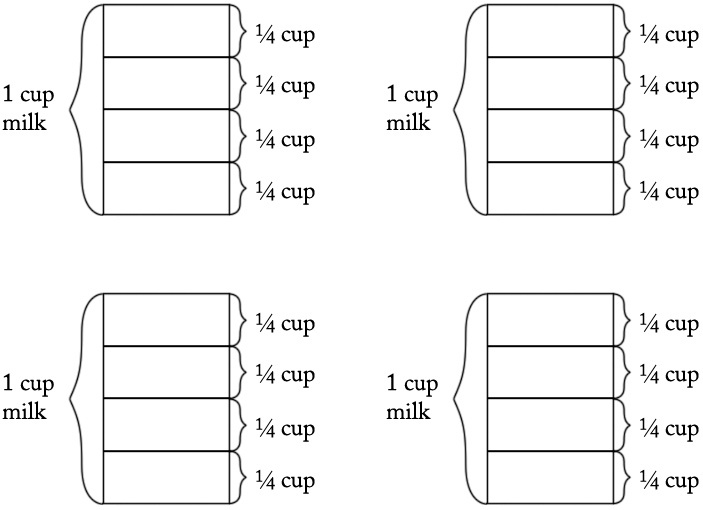
  Again, this is a "how many groups?" division problem because it asks "How many quarter cups are in 4 cups?" There are two correct equations:

  $4÷\frac{1}{4}=?$

  
  or equivalently:

  $?×\frac{1}{4}=4$

  
  We can verify that 16 is the correct solution by noting that $16×\frac{1}{4}=\frac{16}{4}=4$

       c. We can think of this problem several ways. First, we can ask, "How many cups did I start with if i ended up with 12 quarter cups?" We could write an equation for this:

  $?÷\frac{1}{4}=12$

  
  We could also say, "I have 12 quarter cups and I want to know how many cups this is, so I can multiply 12 and $\frac{1}{4}$ to find the number of cups I started with." This can be represented with the following equation:

  $12×\frac{1}{4}=?$

  
  Notice that these two equations are equivalent and can both be interpreted in terms of the following picture: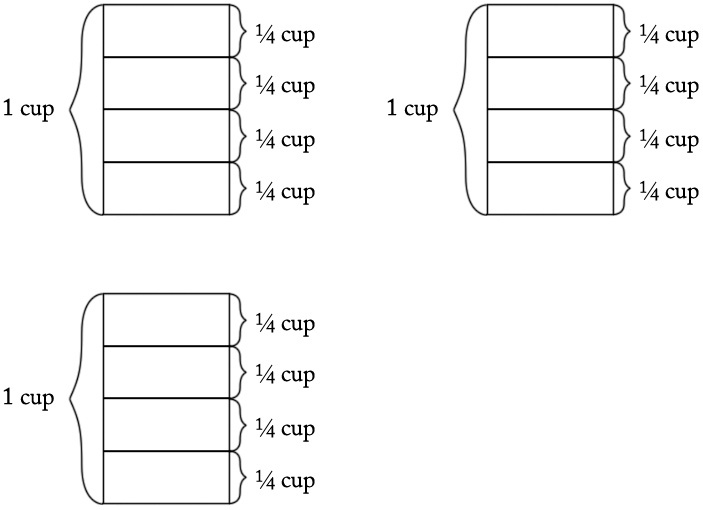
  
  Here is yet another approach: If we note that there are 4 quarter cups in 1 cup, we can also think of this as a "how many groups?" division problem. We know that there are a total of 12 quarter cups and that there are 4 quarter cups in a cup (a group), and we want to know how many cups (or how many groups) this makes. Here the equation is:

  $12÷4=?$

  
  Since $12÷4=3$, she must have started with the vanilla pudding mix, as that is the only ingredient that requires 3 cups.

• Additional Thoughts

Send Feedback