Quadratic Equations Mini-Assessment

Author: Student Achievement Partners

  • Description
  • Files

This mini-assessment is designed to illustrate standards A-REI.B.4and A-CED.A.1, which set an expectation for students to create, use, and solve quadratic equations. This mini-assessment is designed for teachers to use in the classroom, for self-learning, or in professional development settings to:

  • Evaluate students' understanding of A-REI.B.4 and A-CED.A.1 in order to prepare to teach this material or to check for student ability to demonstrate understanding and apply these concepts;
  • Gain knowledge about assessing quadratic equations; and
  • Use in professional development as an illustration of CCSS-aligned assessment problems.

  • Making the Shifts

    How does this mini-assessment exemplify the instructional Shifts required by CCSSM?

    Focus Belongs to the Widely Applicable Prerequisites for College and Careers
    Coherence Builds on work with linear equations (8.EE.C) and functions (8.F.B), representing a capstone of the multi-year progression for finding ways of transforming equations into certain standard forms that have the same solutions
    Rigor

    This mini-assessment touches on all three aspects of rigor: conceptual understanding, procedural skill and fluency, and application.
  • Noteworthy features of this resource
    • Mathematically
      • Demonstrates how these standards address all three aspects of rigor
      • Requires components of the modeling cycle (formulate, compute, interpret)
      • Challenges students to define their own variables in real-world and mathematical problems
    • As a mini-assessment:
      • Offers quick conceptual problems that focus on the properties of equations and quadratics
      • Assesses procedural skill based on understandings of quadratic equations
      • Allows the teacher to evaluate students on their understanding of A-REI.B.4 and A-CED.A.1 in order to prepare to teach A-REI.B.4 and A-CED.A.1 or to check student understanding and progress
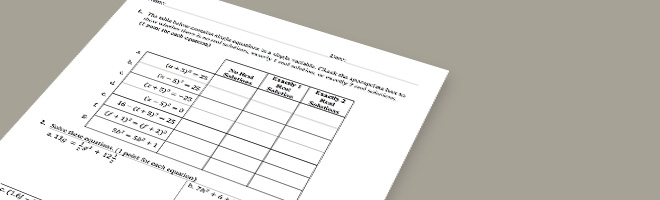
      • Shows equations in various ways (e.g., $(a+5)^2=25$, $5b^2=5b^2+1$, $7h^2+6+2h=h^2+4h+26+5h$, etc.) to ensure students have conceptual understanding in addition to procedural skill

Supplemental Resources