Functions

Define, Evaluate, And Compare Functions.

Major Cluster

8.F.A.1

Understand that a function is a rule that assigns to each input exactly one output. The graph of a function is the set of ordered pairs consisting of an input and the corresponding output.*

^{*Function notation is not required in Grade 8.}

Functions

Define, Evaluate, And Compare Functions.

Major Cluster

8.F.A.2

Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a linear function represented by a table of values and a linear function represented by an algebraic expression, determine which function has the greater rate of change.

Functions

Define, Evaluate, And Compare Functions.

Major Cluster

8.F.A.3

Interpret the equation y = mx + b as defining a linear function, whose graph is a straight line; give examples of functions that are not linear. For example, the function A = s² giving the area of a square as a function of its side length is not linear because its graph contains the points (1,1), (2,4) and (3,9), which are not on a straight line.

Functions

Use Functions To Model Relationships Between Quantities.

Major Cluster

8.F.B.5

Describe qualitatively the functional relationship between two quantities by analyzing a graph (e.g., where the function is increasing or decreasing, linear or nonlinear). Sketch a graph that exhibits the qualitative features of a function that has been described verbally.

Interpreting Functions

Understand The Concept Of A Function And Use Function Notation

Widely Applicable Prerequisite

HS.F-IF.A.1

Understand that a function from one set (called the domain) to another set (called the range) assigns to each element of the domain exactly one element of the range. If f is a function and x is an element of its domain, then f(x) denotes the output of f corresponding to the input x. The graph of f is the graph of the equation y = f(x).

Course Information

Twenty frameworks were reviewed to investigate the course(s) in which this standard is typically addressed.

TRADITIONAL
INTEGRATED

Algebra 1:All or almost all of the frameworks consulted addressed this standard.
Geometry:Few or None of the frameworks consulted addressed this standard.
Algebra 2:Few or None of the frameworks consulted addressed this standard.

Math 1:All or almost all of the frameworks consulted addressed this standard.
Math 2:Few or None of the frameworks consulted addressed this standard.
Math 3:Few or None of the frameworks consulted addressed this standard.

Example Task

The Parking Lot

Provided by Illustrative Mathematics

Task

A parking lot charges $\$0.50$ for each half hour or fraction thereof, up to a daily maximum of $\$10.00$ . Let $C(t)$ be the cost in dollars of parking for $t$ minutes.

a. Complete the table below.

$t$ (minutes)	$C(t)$ (dollars)
0
$15$
$20$
$35$
$75$
$125$

b. Sketch a graph of $C$ for $0 \leq t \leq 480$ .

c. Is $C$ a function of $t$ ? Explain your reasoning.

d. Is $t$ a function of $C$ ? Explain your reasoning.

Solution

$t$ (minutes)	$C(t)$ (dollars)
0	0
$15$	$0.50$
$20$	$0.50$
$35$	$1.00$
$75$	$1.50$
$125$	$2.50$

As a sample calculation, we note that $125$ minutes is two full hours (four half-hours) and part of another half hour. Since the ticketing scheme rounds up to the nearest half-hour, we have to pay for five half-hours, at a total cost of $2.50.

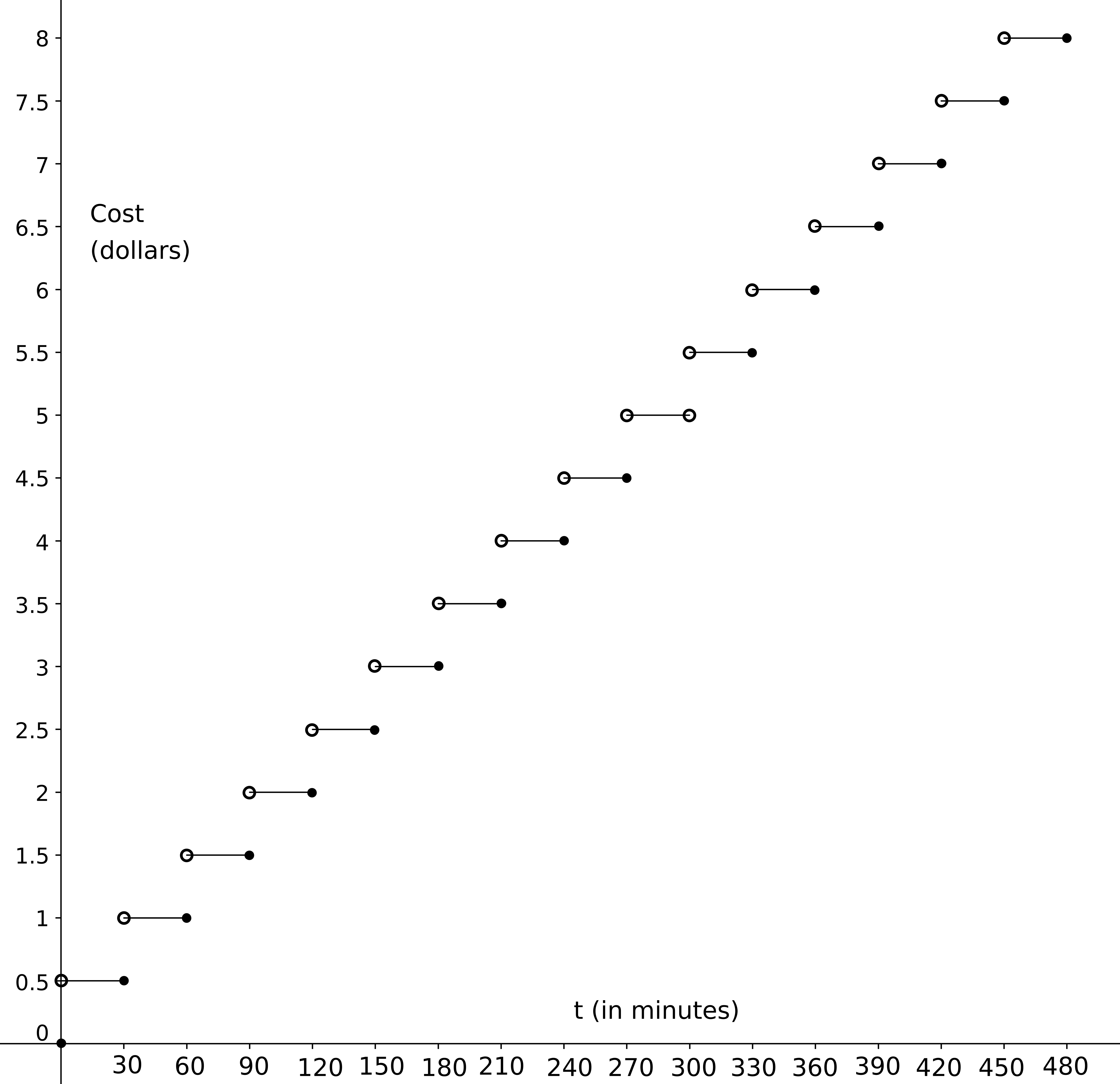
c. Yes, $C$ is a function of $t$ because for a given parking time of $t$ minutes there is exactly one charge.

d. No, $t$ is not a function of $C$ because there are values of $C$ that have many values of $t$ associated with them. For example if you end up paying $\$0.50$ then you could have parked for any period of time up to half an hour, that is, when $C = 0.50$ then $t$ can have any value in the range $0 < t \le 30$ . So the "input" $C = 0.50$ yields more than one output, which is not allowed for a function.

Download Example Task

Progressions

Building on semi-formal notions of functions from Grade 8, students in high school begin to use formal notation and language for functions. Now the input/output relationship is a correspondence between two sets: the domain and the range. The domain is the set of input values, and the range is the set of output values. A key advantage of function notation is that the correspondence is built into the notation. For example, f(5) is shorthand for “the output value of f when the input value is 5.”

Please reference page 7 in the Progression document.

Download Progressions PDF

Tasks

Parabolas and Inverse Functions Finding the Domain Points on a Graph Domains

Prior Grade-Level Tasks

The tasks below align to standards that are critical building blocks to this standard. Students do not necessarily need to be successful with these tasks to be able to engage with this standard, but these tasks can help teachers ground themselves in the skills and knowledge that students are bringing to the current unit of study and gather valuable information to use when teaching this standard. These tasks can be used as homework, warm-ups, in one-on-one work with students, or in PLC discussions. Because of their close ties to the work of this standard, the standards and the tasks below are a good place to start to:

review just before the current unit of study,
surface content that deserves additional support while addressing this standard,
focus the time on readiness for the current unit of study, and/or
provide visibility into a student’s thinking about a related task and determine how best to bring the student into the current unit of study.

8.F.A.1 Function Rules 8.F.A.1 Introducing Functions 7.EE.B.4 Gotham City Taxis

Focus

Widely Applicable Prerequisites – High School

Interpreting Functions

Analyze Functions Using Different Representations

Widely Applicable Prerequisite

HS.F-IF.C.9

Compare properties of two functions each represented in a different way (algebraically, graphically, numerically in tables, or by verbal descriptions). For example, given a graph of one quadratic function and an algebraic expression for another, say which has the larger maximum.

Functions

Use Functions To Model Relationships Between Quantities.

Major Cluster

8.F.B.4

Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.

Linear, Quadratic, And Exponential Models

Construct And Compare Linear, Quadratic, And Exponential Models And Solve Problems

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-LE.A.1

Distinguish between situations that can be modeled with linear functions and with exponential functions:

Interpreting Functions

Interpret Functions That Arise In Applications In Terms Of The Context

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-IF.B.4

For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.

Linear, Quadratic, And Exponential Models

Construct And Compare Linear, Quadratic, And Exponential Models And Solve Problems

Modeling Standard ★

HS.F-LE.A.3

Observe using graphs and tables that a quantity increasing exponentially eventually exceeds a quantity increasing linearly, quadratically, or (more generally) as a polynomial function.

Building Functions

Build A Function That Models A Relationship Between Two Quantities

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-BF.A.1.a

Determine an explicit expression, a recursive process, or steps for calculation from a context.

Building Functions

Build A Function That Models A Relationship Between Two Quantities

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-BF.A.1.b

Combine standard function types using arithmetic operations. For example, build a function that models the temperature of a cooling body by adding a constant function to a decaying exponential, and relate these functions to the model.

Building Functions

Build New Functions From Existing Functions

HS.F-BF.B.4

Find inverse functions:

Interpreting Functions

Understand The Concept Of A Function And Use Function Notation

Widely Applicable Prerequisite

HS.F-IF.A.2

Use function notation, evaluate functions for inputs in their domains, and interpret statements that use function notation in terms of a context.

Interpreting Functions

Interpret Functions That Arise In Applications In Terms Of The Context

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-IF.B.5

Relate the domain of a function to its graph and, where applicable, to the quantitative relationship it describes. For example, if the function h(n) gives the number of person-hours it takes to assemble n engines in a factory, then the positive integers would be an appropriate domain for the function.

Interpreting Functions

Analyze Functions Using Different Representations

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-IF.C.7.a

Graph linear and quadratic functions and show intercepts, maxima, and minima.

Interpreting Functions

Analyze Functions Using Different Representations

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-IF.C.7.b

Graph square root, cube root, and piecewise-defined functions, including step functions and absolute value functions.

Interpreting Functions

Analyze Functions Using Different Representations

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-IF.C.7.c

Graph polynomial functions, identifying zeros when suitable factorizations are available, and showing end behavior.

Interpreting Functions

Analyze Functions Using Different Representations

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-IF.C.7.d

(+)

Graph rational functions, identifying zeros and asymptotes when suitable factorizations are available, and showing end behavior.

Interpreting Functions

Analyze Functions Using Different Representations

Widely Applicable Prerequisite

Modeling Standard ★

HS.F-IF.C.7.e

Graph exponential and logarithmic functions, showing intercepts and end behavior, and trigonometric functions, showing period, midline, and amplitude.

Trigonometric Functions

Extend The Domain Of Trigonometric Functions Using The Unit Circle

HS.F-TF.A.2

Explain how the unit circle in the coordinate plane enables the extension of trigonometric functions to all real numbers, interpreted as radian measures of angles traversed counterclockwise around the unit circle.

Congruence

Experiment With Transformations In The Plane

Widely Applicable Prerequisite

HS.G-CO.A.3

Given a rectangle, parallelogram, trapezoid, or regular polygon, describe the rotations and reflections that carry it onto itself.

Congruence

Experiment With Transformations In The Plane

Widely Applicable Prerequisite

HS.G-CO.A.4

Develop definitions of rotations, reflections, and translations in terms of angles, circles, perpendicular lines, parallel lines, and line segments.