“Problem solving.”
Be honest: haven’t you, at times, used these words to signal problems you would skip at the end of each section of your book? Don’t feel bad — we’ve all done it. It’s what we thought — or were told — was best. Problem solving is important though!
As educators, we want instructional materials that promote engagement in problem solving. As students problem solve, they need the skills that were discussed in Standard for Mathematical Practice (SMP) 1 (make sense of problems and persevere in solving them), and also need to reason abstractly and quantitatively. This abstract and quantitative reasoning is covered in SMP 2.
The two buzzwords when talking about SMP 2 are “contextualize” (taking the abstract mathematical representation and putting into context), and “decontextualize” (taking context and representing it abstractly). Students need to move between these representations fluidly and use them to manipulate and understand the relationships between the quantities. This idea relates primarily to abstract reasoning but we cannot forget quantitative reasoning. While engaging in quantitative reasoning, students pay attention to the meaning of quantities they compute and also to the units involved.
Obviously, instructional materials for different grade levels will have some commonality in how opportunities to engage in SMP 2 will appear. However, the complexity of the problems will increase as well as the depth at which students are expected to connect the quantitative and abstract reasoning.
As you can see in the grade 2 example below, students need to decontextualize the problem to write the equation 53 + 34 = __, showing abstract reasoning. They also need to attend to the fact that the result they get, 87, actually means $87.
Problem designed by the author.
As we look at the next example from grade 7, we see students engage in many of the same skills related to SMP 2 as they do in earlier grades. Students are decontextualizing the problem, producing a symbolic representation, manipulating those symbols, and putting it back into context. We see that students are being asked to make sense of their abstract solution in context. Additionally, we see the need to repeatedly move between the context and abstract representations.
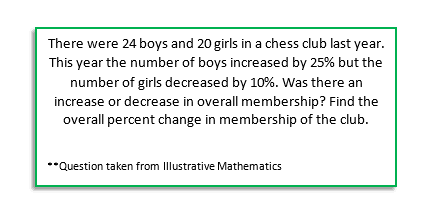Problem from Illustrative Mathematics. Accessible here: https://www.illustrativemathematics.org/content-standards/7/RP/A/3/tasks/130
Looking at high school materials and SMP 2, we see students begin to deepen their understanding of various parameters and how changing those parameters changes the situation. We can see an example of this below.
Problem from Illustrative Mathematics. Accessible here: https://www.illustrativemathematics.org/content-standards/HSF/LE/B/5/tasks/579
In looking at the above examples, you might recognize other math practices as well. Remember that the Standards for Mathematical Practice are not intended to be taught in isolation. While you may see some questioning that helps students build their abilities in one specific math practice, you should also see opportunities to engage in multiple math practices simultaneously. This balance reflects how students will need to use their skills in real world scenarios.
Problem designed by the author.
“Remember that the Standards for Mathematical Practice are not intended to be taught in isolation.”
This quote stood out to me in the fact that we can’t expect our students to only look at math through one lens. We can alleviate math anxiety by empowering students to use their preferred skills when approaching a problem. This will look different for every student. finding that real life connection is also key in setting them up for success.