When I first started teaching third grade almost 20 years ago, my students and I loved the fraction unit in math! We all thought it was fun because I could bring in lots of great manipulatives (including food sometimes!) to help my students understand fractions. One year I bought ice cream sandwiches and after my students spent some time cutting them up into various numbers of equal sized pieces, and before the ice cream melted, the students got to eat parts of about 3/4 of the ice cream sandwiches!
I learned fractions myself when I was in grade school by working with representations such as pizzas, pies, and cakes. I remember countless worksheets where I was given shapes to split up into equal pieces and shade to make fractions. I then taught my own students the same way I learned and in the way the textbooks guided me. I now realize this emphasis on fractions being parts of a whole object or sets of objects, while fun and engaging, was not helpful for my students.
Like me, you probably weren’t taught fractions the right way, either.
The thing is, fractions are how we describe part of a whole; however, they are much more than that. Fractions are numbers. Fractions have distinct quantities. They have value and can be compared, ordered, and placed on a number line. Down the road, when students start to add, subtract, multiply, and divide fractions, it could be confusing for them to make sense of operations such as multiplying with a piece of pizza. However, it makes sense to multiple with numbers. Students have already multiplied with whole numbers. If they understand fractions as numbers also, it makes perfect sense to multiply fractions.
Consider this task from Illustrative Mathematics:

Students who understand that fractions are numbers will recognize that 2/3 is a quantity made up of two 1/3s and that 2/3 is 1/3 less than 1, and they will be able to select a representation for 5 x 4 that can also be used to represent 5 x 2/3. They will also likely be able to reason that the product will be less than 5 and explain their reasoning.
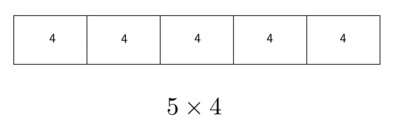

In these representations, students can make sense of both problems as having five groups of a quantity. In one case, the quantity is 4; but in the other case, the quantity is 2/3. The concept of groups that students began learning about in third grade related to multiplicative thinking can be extended when they start working with fractions. Leveraging previous understanding about multiplication of whole numbers can help students make sense of multiplication of fractions. This type of mathematical coherence is needed for students to carry mathematical concepts and ideas forward for success in Algebra.
Siegler et al. found that “elementary school students’ knowledge of fractions predicts their mathematics achievement in high school, above and beyond the contributions of… verbal and nonverbal IQ, working memory, family education, and family income.” Students who leave elementary school with a deep understanding of fractions are likely to be successful in high school mathematics.
Another important feature of numbers that is true for both whole numbers and fractions is that they can be composed and decomposed. In fact, students spend significant time in grades K-2 thinking about the place value system: for example how ten is composed of ten ones or how one hundred can be decomposed into many combinations of tens and ones. The idea of units, like ones, tens, and hundreds, continues into fractions when students start to learn that unit fractions (for example, 1/6) can be composed to make other fractions (such as 5/6 or 7/6). When I learned about fractions as a student, I know mixed numbers and “improper” fractions were introduced as new, separate concepts from fractions. In fact, they are all numbers.
I once asked a student, Parker, to complete a task that asked him to place the number 1 on a number line that showed two numbers, 0 and 5/3 (video available here).
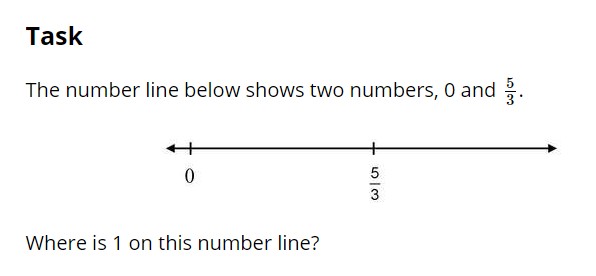
Right away I could tell Parker was uncomfortable with 5/3 and not used to seeing fractions on a number line. Here is how our conversation went:
Teacher: Okay, Parker, so read the problem.
Parker: Task- The number line below shows two numbers, zero and five… [pause] three-fifths.
Teacher: Five-thirds
Parker: Five-thirds. So this should be one. [writes 1 at the end of the number line] This should be one. So right here, this would be one-third [marks near the zero], this would be two-thirds, [number marks moving toward the 5/3] so this would be three-thirds, this would be three-thirds [writes 4/3].
Teacher: Four-thirds, you mean?
Parker: Four-thirds.
Teacher: Okay, so look at the numbers you wrote there, all the fractions.
Parker: One-third, two-third, three-third, four… [shakes head, starts over] One-third, two-third… [pause, repeats] two-thirds, three-thirds, and four-thir… four-thirds.
Teacher: Okay, so where do you think one is again?
Parker: So, it’s not right there [erases 1 at the end of the number line], it’s right here [writes one above 5/3].
Teacher: Is five-thirds the same as one?
P: Five-thirds? [long pause, looking at paper] Yes.
Right away when looking at the task, Parker flipped 5/3 and said three-fifths. He continued to struggle later when he tried to read 4/3 in the count from one-third. Parker also was not clear where 1 fell in relation to 0 and 5/3. He assumed 1 would naturally go at the end of the line.
By spending time with 3.NF.A.1 (Understand a fraction 1/b as the quantity formed by 1 part when a whole is partitioned into b equal parts; understand a fraction a/b as the quantity formed by a parts of size 1/b.) students are able to make sense of fractions greater than one. Students can reason about the value of fractions less than and greater than one. Students who understand that fractions that are built out of unit fractions, say 5/3 as being five, one-thirds or 1/3+1/3+1/3+1/3+1/3, can make sense of not only where the number one goes on the number line, at the point they have combined three one-thirds, but also why it makes sense to even have a number like five-thirds represented on a number line.
Later on in elementary or middle school when students encounter fractions greater than one when they are operating with fractions or when they work with fractions in algebraic equations, they understand the value of the fractions and products or quotients make sense.
By focusing on fractions as numbers and helping students make sense of fraction values, including emphasizing unit thinking, teachers can set students up for high school success. This is different from the way I was taught, as well as many other teachers I know, and it is likely different from the ways we have taught students in the past. However, as we dig into mathematical content knowledge and learn more about important math topics, we can do better for kids to set them up for math success.

















When I see a video on YouTube that demonstrates for teachers the Five great ways to teach fractions and not one uses a number line or at best it is the last choice mentioned I realize it is not the students fault they don’t know or like math, it is the lack of commitment to what works and the lack of determination to ensure that it is taught correctly!
I completely agree with you. I am a K-9 math interventionist now, but taught 6-12 math for 19 years prior. I see the worst of it in middle school actually, but definitely in lower grades as well. Most middle level math teachers hold a k-8 license. Which, in my state anyway, means they can teach any subject. The “horror” of this is clearly seen in mathematics. I cannot tell you how many times I have had to “fix” math knowledge for students coming into middle school or when they get to high school. I am not trying to bash anyone. This is a systemic problem. The problem is that the teachers do not have enough knowledge in mathematics to teach it correctly because they haven’t seen how fractions are connected to all things, especially when it comes to algebra concepts. It is a disservice to the teachers and to the students. More math requirements need to be implemented in teacher programs if this is going to change and it definitely needs to include this approach.
A deficit view of elementary teachers and elementary credentials is more concerning in this comment than the fraction instruction. I’ve taught secondary, elementary, middle, university, and what is true is ALL teachers can teach deeply. Many need additional support to explore these concepts, but that “many” is at any level with any credentials!
Great post, thank you for sharing this…
Hi there. As a K-5 Math Coach, I completely agree that most folks were never taught the conceptual meaning that underlies fractions ( I know I was not)! As I go deeper into my own understanding and bring this forward to the amazing teachers I work with it is a win-win for the adults who will bring this knowledge into their classrooms. we are starting this year with Equal Sharing in Kinder and the teachers are really enjoying and so are their students.
7th grade teacher; the best method I’ve used to make students see fractions as numbers is to always make “whole” numbers fractions. Ie: They don’t see 2 written as 2/1 enough.
Thank you for your clear and thought-provoking article. I am just starting as a math interventionist, and my main problem right now is helping sixth graders fill in 3 years worth of gaps in their understanding of fractions.
Clearly these students have been taught procedures each year to get the right answer to all things that can be done to or with fractions. However, now it is painfully obvious they have no in-depth understanding of fractions as numbers. These sixth graders are not able to compose and decompose common fractions or to demonstrate relationships between and among fractions and whole numbers. That leaves them with bits and pieces of procedures floating around in their heads, but with terrible misconceptions about how and when to apply those procedures.
Even worse, as a third grade teacher I was guilty of instilling some of those misconceptions into young minds. I thought I knew math and had actually had some very good training. With parts of a whole or parts of a set. When the Common Core and then new State standards stressed teaching fractions on a number line I couldn’t figure out why that was so important (and it seemed like One More Thing). So I accommodated this new addition with … more procedures.
Your article and my own experience point out the critical need for all teachers to learn the progression of concepts through the grades and also see how their part contributes later success.
Thank you, #achievethecore for resources that help us all improve instruction by learning more math and seeing more connections while also providing student tasks that point the way!
Thank you for the enlightenment! It definitely helps me tighten up on my own instructions and explains why my sixth graders have the deficits they do. Where I understand the importance and depth of teaching fractions, I will do a better job assisting my colleagues. Each one teaches one.