There’s so much to do. What should we focus on?
Lots of things matter. You need a rich curriculum. You’ll be driven crazy if the assessments aren’t aligned, and things will be difficult if administrators don’t support what you’re doing. But let’s narrow down to your teaching. Say you had to pick five things to focus on when planning to teach. What would they be?
The Teaching for Robust Understanding (TRU) framework (see Figure 1) highlights five essential dimensions of teaching. If you get these right, your students will be knowledgeable and resourceful thinkers and problem solvers.
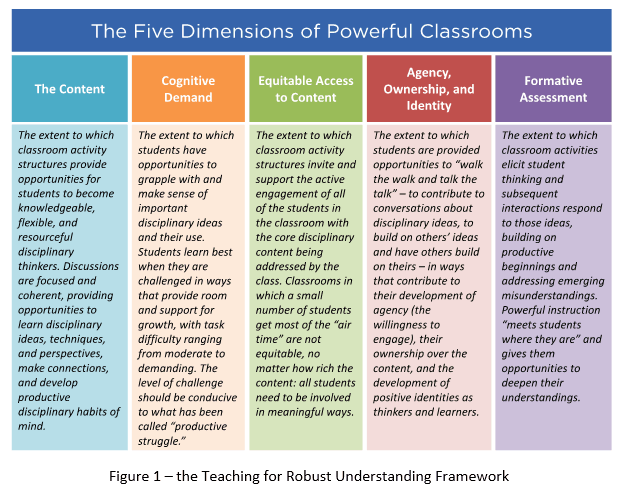 Dimensions 2 through 5 focus on the student experience. That shouldn’t come as a surprise: it’s the students who are doing the learning, after all. So, they’d better have opportunities for sense making, at a level that they can engage with. If things are too easy, or too hard, they can’t engage in “productive struggle” (dimension 2, cognitive demand). We want all students to have meaningful opportunities to learn (dimension 3 equitable access to content) – and, opportunities to do so in which they get to refine their ideas in collaboration with others, in ways that allow them to see themselves as disciplinary thinkers (dimension 4, agency, ownership, and identity). After all, a positive disciplinary identity, whether as a writer, a scientist, a historian – you name it! – comes from engaging meaningfully with the discipline. And, of course, if the students reveal what they know, it’s much easier to meet them where they are. That’s what formative assessment (dimension 5) is all about. There’s loads of documentation for these claims; see [References 1,2]. More important, there are tools to help get better at this – see an introduction at [Reference 3] and tools such as these conversation guides [References 4,5] and observation guides [References 6,7].
Dimensions 2 through 5 focus on the student experience. That shouldn’t come as a surprise: it’s the students who are doing the learning, after all. So, they’d better have opportunities for sense making, at a level that they can engage with. If things are too easy, or too hard, they can’t engage in “productive struggle” (dimension 2, cognitive demand). We want all students to have meaningful opportunities to learn (dimension 3 equitable access to content) – and, opportunities to do so in which they get to refine their ideas in collaboration with others, in ways that allow them to see themselves as disciplinary thinkers (dimension 4, agency, ownership, and identity). After all, a positive disciplinary identity, whether as a writer, a scientist, a historian – you name it! – comes from engaging meaningfully with the discipline. And, of course, if the students reveal what they know, it’s much easier to meet them where they are. That’s what formative assessment (dimension 5) is all about. There’s loads of documentation for these claims; see [References 1,2]. More important, there are tools to help get better at this – see an introduction at [Reference 3] and tools such as these conversation guides [References 4,5] and observation guides [References 6,7].
How much do disciplinary knowledge and disciplinary tools (for example, observation rubrics) matter? After all, don’t four of the five TRU dimensions look discipline-free?
Well, they may look that way, but they’re not. That’s because each of the dimensions lives by way of the disciplinary opportunities made available to the students—and how that happens in math, for example, is very specific to mathematics.
I’ll illustrate this using my own disciplinary strengths and weaknesses. I’m pretty good at math, and I have a lot of what’s been called “pedagogical content knowledge” in math – I know what the implications of student thinking are; I know what ideas are productive, and which ones lead to dead ends; I have a good understanding of what it means to connect mathematical ideas. I “get” the standards, so I can help make them come alive in my classroom. I might not do too badly at ELA because I’ve spent a lot of time working on related issues. But, I don’t have a deep enough understanding of social studies or history to help my students experience those disciplines in rich ways, and when it comes to some of the sciences, well, forget it – my knowledge is superficial. I could master the facts and formulas, but when it comes to supporting deep understanding in my students… you’d want someone who really gets it, not me.
What does this say about TRU, and about observation tools in general? Knowledge of the discipline, and of student thinking in it, become central as soon as you dig into each dimension. How do I know what’s easy or hard (cognitive demand)? How do I know where students can gain entry into the content (equitable access), or debate productively (agency, ownership, identity)? How do I know what to listen for, and how to adjust my instruction? The more I know about the content and student thinking in it, the better I can address these issues.
In fact, deep disciplinary understanding plays out with regard to curriculum, assessment, and coaching and classroom observations. The best curriculum materials I know pay deep attention to the content riches, and to student thinking. Take a look at the Formative Assessment Lessons at the Mathematics Assessment Project website [Reference 8]. What makes them so powerful [References 9,10] is that they’re aimed at deep understanding of the content, and grounded in an understanding of the things students are likely to understand and misunderstand. Regarding assessment, Hugh Burkhardt’s phrase WYTIWYG – “What You Test Is What You Get – is all too true. Dumbed-down tests aim us in the wrong directions, while rich tests help us measure what matters. And if I’m to have help from colleagues when I want to improve my teaching, what I’d like are colleagues who “get” both the content I’m teaching and student thinking in the discipline. I need tools that help in similar ways – tools that help me focus on what counts in my classroom. Compelling arguments in mathematics (“proofs”) are different from rigorous arguments in literature, or in science classrooms, for example. Misconceptions are content-specific. Tools are more powerful if they’re tailored to my needs. So, let’s focus on the big ideas, such as the TRU dimensions – AND, let’s build more discipline-specific tools, such as observation tools and discussion guides, that help us dig into the specifics of what we teach.
References
[1] Schoenfeld, A. H. (2013). Classroom observations in theory and practice. ZDM, the International Journal of Mathematics Education, 45: 607-621. DOI 10.1007/s11858-012-0483-1.
[2] Schoenfeld, A. H. (2014, November). What makes for powerful classrooms, and how can we support teachers in creating them? Educational Researcher, 43(8), 404-412. DOI: 10.3102/0013189X1455
[3] Schoenfeld, A. H., & the Teaching for Robust Understanding Project. (2016). An Introduction to the Teaching for Robust Understanding (TRU) Framework. Berkeley, CA: Graduate School of Education. Retrieved from http://map.mathshell.org/trumath.php or http://tru.berkeley.edu.
[4] Baldinger, E. Louie, N., and the Algebra Teaching Study and Mathematics Assessment Project. (2016). TRU Math conversation guide: A tool for teacher learning and growth (mathematics version). Berkeley, CA & E. Lansing, MI: Graduate School of Education, University of California, Berkeley & College of Education, Michigan State University. Retrieved from: http://ats.berkeley.edu/tools.html and/or http://map.mathshell.org/materials/pd.php.
[5] Louie, N., Baldinger, E. and the Algebra Teaching Study and Mathematics Assessment Project. (2016). TRU Math conversation guide: A tool for teacher learning and growth (Domain-general version). Berkeley, CA & E. Lansing, MI: Graduate School of Education, University of California, Berkeley & College of Education, Michigan State University. Retrieved from: http://ats.berkeley.edu/tools.html and/or http://map.mathshell.org/materials/pd.php.
[6] Schoenfeld, A. H., and the Teaching for Robust Understanding Project. (2016b). The Teaching for Robust Understanding (TRU) observation guide for mathematics: A tool for teachers, coaches, administrators, and professional learning communities. Berkeley, CA: Graduate School of Education, University of California, Berkeley. Retrieved from: <http://TRU.berkeley.edu> or <http://map.mathshell.org/> or <http://ats.berkeley.edu/>.
[7] Schoenfeld, A. H., and the Teaching for Robust Understanding Project. (2016a). The Teaching for Robust Understanding (TRU) observation guide: A tool for teachers, coaches, administrators, and professional learning communities. Berkeley, CA: Graduate School of Education, University of California, Berkeley. Retrieved from: <http://TRU.berkeley.edu> or <http://map.mathshell.org/> or <http://ats.berkeley.edu/>.
[8] Mathematics Assessment Project. Formative Assessment Lessons, at http://map.mathshell.org/lessons.php.
[9] Herman, J., Epstein, S., Leon, S., La Torre Matrundola, D., Reber, S., & Choi, K. (2014). Implementation and effects of LDC and MDC in Kentucky districts (CRESST Policy Brief No. 13). Los Angeles: University of California, National Center for Research on Evaluation, Standards, and Student Testing (CRESST).
[10] Research for Action. (2015). MDC’s Influence on Teaching and Learning. Philadelphia, PA: Author. Retrieved March 1, 2015 from https://www.researchforaction.org/publications/mdcs-influence-on-teaching-and-learning/
















