Fractions play a prominent role in students’ mathematical understanding and are part of the Major Work of elementary mathematics in grades 3-5. Knowing this, we decided to make fractions the content and context of a professional learning experience for teachers and students called Fraction Lab. You can read more about Fraction Lab here. This professional learning experience included pedagogies of investigation and enactment. When we first began to plan for the experience, we considered the students we would be working with as well as the instructional materials available.
From the lens of instructional materials, it was important to us to use high-quality aligned materials in our work with students, materials that would ensure access to the standards. We began by exploring the district-adopted instructional materials to understand what was available to us, how fractions were addressed, and how well aligned the materials were (specifically in regards to fractions) to the expectations of the standards.
We read the EdReports review for the district-adopted program and examined the fraction units in both third and fourth grades. Both EdReports and our own review identified limited attention to the CCSS third grade cluster heading in the Number and Operations Fractions domain: “Develop understanding of fractions as numbers.” For example, the third grade EdReports review states, “Fractions as Fair Shares and Fractions on a Line Plot; these are the first two fractions modules in Grade 3 and could have attended more closely to the cluster heading, ‘Develop an understanding of fractions as numbers.’” Through our Fraction Lab work, we hoped to identify ways to build this understanding that could then be used to adapt the curriculum.
To prepare for our work with students exiting third and fourth grades, we developed a pre-assessment to identify student strengths and select content to focus on in our summer math lab. The pre-assessment included tasks that would make student thinking visible and included content foundational to fourth and fifth grade fraction concepts including;
- Understanding fractions as numbers
- Naming fractional parts
- Comparing fractions
- Understanding equivalence
- Plotting fractions on a number line
As we looked at student work on the pre-assessment, two things resonated with us as things we’d seen often in the field: student misunderstandings around the concept of fractions as numbers and student misunderstandings around plotting fractions on the number line. One particular set of questions we posed–Is a fraction a number? How do you know?– yielded particularly interesting information. Most students responded, “No, a fraction is not a number,” and of the few that said “Yes, a fraction is a number,” many reasoned that a fraction is a number “because it has numbers in it.” As a result, we identified this as one area of focus within our summer Fraction Lab.
The pre-assessment also included two number lines, each with 0 plotted along with one other fraction. One number line included 0 and 1/4 and the other, 0 and 5/3. Students were asked to plot 1 on each of the number lines. Almost all students plotted 1 at the end of each number line and many included comments like, “1 is always at the end of a number line.” This caused us to wonder where this misconception came from. We began by looking at the district’s instructional materials and found that every number line in the third grade curriculum, whether on a practice page, part of the core program, or an assessment, had a 1 at the end of the number line. We knew this was something we needed to address within our work.
These two noticings led us to select two instructional activities that would be used daily within our work with teachers and students, a yarn number line and choral counting. (See the next post in this series to learn more about the yarn number line and how it can be used to build student understanding of fractions.)
We selected choral counting as an instructional activity because it would contribute to student understanding of fractions as numbers and could also be leveraged to build other important fraction understandings including comparing fractions and equivalence. In addition to the affordances choral counting could offer students, we saw this as an opportunity for teachers to work on instructional practices including eliciting, interpreting, and responding to student thinking. The predictability of the routine would make participation accessible to students and provide teachers with opportunities to focus their planning efforts on pedagogical moves.
What is choral counting?
Choral counting is an instructional routine in which students count aloud together and the teacher strategically records the counting sequence. Within the routine, students experience the cadence of counting aloud, explore the counting sequence, and notice and make sense of patterns and structures within the count and our number system. The teacher pauses the count at periodic points, inviting students to share strategies for identifying the next number, patterns they notice and why those patterns may be occuring, and other mathematical noticings.
To see a choral count in action, click here.
Dropping into a classroom
Let’s drop into a classroom to think about the mathematical affordances of a choral count. This particular count was the first choral count the teacher and students engaged in together. Students and teacher chorally counted by 1/2 beginning at 1/2. As the students counted, the teacher recorded student contributions. The goal of the count was to understand fractions as numbers. For many students, this was the first time they had counted by fractions.
Students and teacher choral counted from ½.
All: 1/2, 2/2, 3/2, 4/2, 5/2, 6/2, 7/2, 8/2, 9/2, 10/2, 11/2, 12/2 (and then the count paused).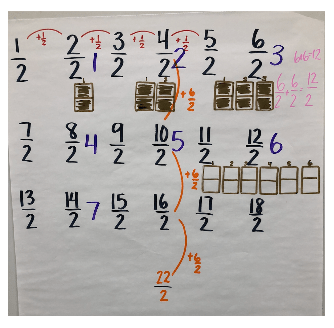
Teacher: What do you notice?
Mariella: It goes like 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
Teacher: So that’s interesting, Mariella says it goes 1…are you looking at the numerator? 1, 2, 3, like that? So that’s kind of interesting, it’s increasing. It’s going up by 1, but it’s going up by 1 what? What’s it going up by? So Mariella’s noticing the numbers are going up by 1, 2, 3, 4…
Student: Adding up.
Teacher: It’s adding, so is it actually going up by 1, or is it 1 of something? Does anybody have an idea? What’s it going up by, like 1 what?
Gianna: It’s going on by 1/2.
Teacher: Ah by ½ (writes on board). So we’re adding 1/2,. Are we adding 1/2 here (pointing to count on chart) to get from 2/2 to 3/2?
Students: Yeah.
Teacher: And Mariella, were we adding ½ to get from 3/2 to 4/2? And how about here, to get from 4/2 to 5/2?
Within this exchange, Mariella and her peers are making connections from whole number thinking to fraction thinking.
As the count continued, a student noticed that 6+6 = 12, perhaps connecting the idea that you can operate on whole numbers with the idea that you can operate with fractions.
Teacher: Brianna, what do you notice?
Brianna: Every number is adding 6.
Teacher: Every number?
Brianna: Like 6+6 is 12. It’s adding the…into the numerator.
Teacher: So I feel like you’re looking, like 6/2 and 12/2, is that what you’re thinking about?
Brianna: So 6+6 equals 12.
Teacher: That’s interesting, so 6 and 6 equals 12, but I think we talked about, we were working in halves, so 6/2 + 6/2 is 12/2? You think that’s connected? So here’s what I heard you say…I heard you say 6+6 is 12. And then I think about this as 6/2, so do you think 6/2+6/2, like could I write this (writes on board) equals 12/2? That’s interesting.
Later in the count, students notice that 2/2 is the same as 1 whole. Another student said 14/2 is a whole number and the teacher posed: “How many wholes in 14/2 and how do you know?” The following discussion emerged:
Teacher: Who has a thought? Ashley, what do you think?
Ashley: 7.
Teacher: 7/2. Or I’m sorry, 7 wholes. So who else thinks it’s 7? Gianna agrees and Brianna, Anthony, Alondra. Ashley, how did you think about 7? How did you know it was 7?
Ashley: I was looking at…and I noticed that you add 6+6 it’s 12…12. It’s a half. So I did the same for 14, and I figured out that it was 7.
Teacher: So you said half of 12 is 6, and so you used that thinking to say half of 14 is 7. So if that thinking works, Ashley, what if we said 16/2. How many wholes is that? Ashley’s telling us something really interesting. Well 12, half of 12 is 6. Half of 14 is 7. And then I asked, well if that thinking works…8. Hmm what do you guys think? Gianna, do you agree with her?
Within the three excerpts from the first choral count experience of Fraction Lab, the opportunities for students to construct an understanding of fraction concepts is evident. Students counted by fractions (a new experience for most participating students), saw connections between the way fractions and whole numbers work, identified fractions equivalent to a whole, and began to notice the relationship between numerators and denominators as they noticed half of 14 is 7 and half of 12 is 6, connecting the concept of half and dividing by 2. The experience also provided opportunities for the teacher to connect fraction representations (area models and numeric), elicit student thinking, and use student thinking to leverage and build the understandings of the group.
Planning a choral count
To plan a choral count, there are several things to consider.
- Identify a mathematical learning goal. What do you want students to explore and learn through the count? The goal of the count situated within this blog was for students to understand fractions as numbers. We hypothesized that counting by a fraction would partially build the understanding that you can count by fractions in the same ways you can count by whole numbers.
- Determine the number to count by and what number to start with. For this particular count, we decided to count by ½ beginning at ½. We made this decision because students had experience with the concept of half and we wanted to build on their knowledge and understanding. We decided to start at ½ both to build on what students already know and also to make visible how the number system works.
- Consider how you will record the count. What patterns do you want students to notice? Thinking about what you want students to notice, how will you record numbers–vertically or horizontally? How many numbers will be in each row or column to make the patterns visible? We decided to record the numbers horizontally in our count and to record six numbers per row. This would leave each row ending with a fraction that’s equivalent to a whole, a pattern we thought students would likely notice.
- Think about check-in points to pause and elicit student ideas. These pause points can be a space for making visible the strategies students are using to determine the next number in the sequence, eliciting student noticings and notating them so other students can see, and discussing mathematical ideas that emerge from student noticings.
- Determine how you will close the count. Decide at what number you will end the count. When will enough numbers be recorded so that students will see and understand the patterns and mathematical ideas embedded within the count?
- Plan discussion of mathematical noticings and patterns. Plan questions you will ask to make student thinking visible as students notice and discuss patterns within the count. Some great starting points can be: What do you notice? What patterns do you see? Why do you think that’s happening? Consider mathematical ideas present within the count and questions that might elicit those ideas. For example, in the context of the count described above, consider questions that can elicit specific fraction ideas, Which fractions are greater than 1? How do you know? Which fractions are equivalent to whole numbers? What whole number is it equivalent to? How do you know?
We have created a planning template that’s helped us in planning choral counts.
Enacting a choral count
To enact a choral count, consider how you will support students to participate. Explain to students that they will count together chorally and you will be recording the count. Explain that, at times, you will pause the count to elicit and record their ideas. Here’s an example of how we introduced students to choral counting.
Teacher: If we’re counting by 1/2, what would come next?
Student: 2
Teacher: 2 what?
Student: Oh I was counting on…1.
Teacher: So we’re counting halves, so 1/2…
Student: 1 and then 1…
Teacher: We’re counting by halves.
Student: Yeah, so a half, then another half equals 1.
Teacher: So 1/2 and another 1/2. We could think about that as 1. We could also think about it as 2/2. So here’s the way this choral count routine works. We’re going to count together, so I need everyone helping. Ready?
Ashley: 1/2, 2/2, 3/2, 4/2, 5/2.
Teacher: Ok, I’m gonna ask you to pause right there because you’re going to count faster than I can write. So we’ve got 6/2, so let’s start again, and then I…we’re gonna keep going. Ready?
Ashley: 1/2, 2/2, 3/2, 4/2, 5/2, 6/2, 7/2, 8/2, 9/2, 10/2, 11/2, 12/2…
Teacher: We’re going to stop right here. We’re going to take a little pause. I’m going to ask you to look at these numbers up here. See if there’s anything that you can use, if there’s any patterns. I’m gonna give you what’s called private think time, so you don’t have to put your hands up. Just think about something that you might notice, and when you notice something, you can show me that you’ve noticed one thing, or you can show me that you’ve noticed two things. So I’m gonna ask everybody to look up here, and see if there’s anything interesting that you notice. When you do, just show me with your thumb. Mariella, do you notice something?
You may notice within the transcript that we introduced the idea of choral counting and how to participate within the actual instructional activity. Students learned by doing with support for how to participate embedded within the experience.
Reflecting on the Experience
As we reflect on our experience using choral counts to develop and extend student and teacher learning through the instructional routine, we consider two lenses: a mathematical lens and a pedagogical/sociocultural lens. From a mathematical lens, we think about the opportunities for students to be sensemakers, to further understand our number system and see fractions as numbers and how they fit into the number system. One aspect we would add to our work is an opportunity for students to reflect on their learning. Could we further advance student thinking about the mathematics by posing questions such as;
- What did you learn from today’s choral count?
- How are fractions like whole numbers?
- Is a fraction a number?
From a pedagogical and sociocultural lens, we see choral counts leveraging students as contributors to a mathematical community of learners. It is the ideas and contributions of the students that are taken up by the teacher and peers to advance the learning of the group. Students are positioned as mathematically smart and they engage in each other’s ideas, learning from and with the group.
Try a choral count and let us know what you learn. We look forward to continuing the conversation! Find us on Twitter: @jenniebeltro @jody_guarino






















Years ago, I worked with a math coach who shared this strategy. I lost the list and wasn’t able to get in touch with her again when I changed grade levels and wanted the other counts that I hadn’t used because they weren’t ideal for my grade level (I believe she had retired). She gave us a great list of suggested counts (whole numbers and fractions), by grade, and that supported different mathematical content pieces for those grade levels. Do you have something like that that you are able to share? I’ve searched a few times over the years since then and this is the first time I’ve even found a reference to the exact strategy!
Thanks!
Awdrey