As teachers, we want to help all kids learn and when we’re faced with the realization that some students just aren’t “getting it,” we work to figure out how to catch kids up. It’s a prevalent struggle many educators grapple with and a frequent conversation in schools: How do we address unfinished learning in math and fill gaps in student understanding?
Over the course of my career I have seen, all too often, students behind grade level denied access to grade-level mathematics, in an effort to catch them up or “fill the holes.” All students deserve access to content-rich instruction at their grade level, and when students have unfinished learning from previous grades, teachers need to take appropriate action—and that doesn’t mean reverting solely to materials and content from previous grades.
So, how do we address unfinished learning and support students in developing understanding and mastery of content? Chrissy Allison, Director of Math Professional Learning at Achievement Network (ANet), and I were knee deep in conversations centered on unfinished learning when we first penned a “Do’s and Don’ts Chart” for catching kids up. The chart identifies some missteps districts, schools, and teachers make when working with students who have gaps in their math knowledge. We’ve included some recommendations to consider to avoid these missteps. You can download the chart at the top of this blog post.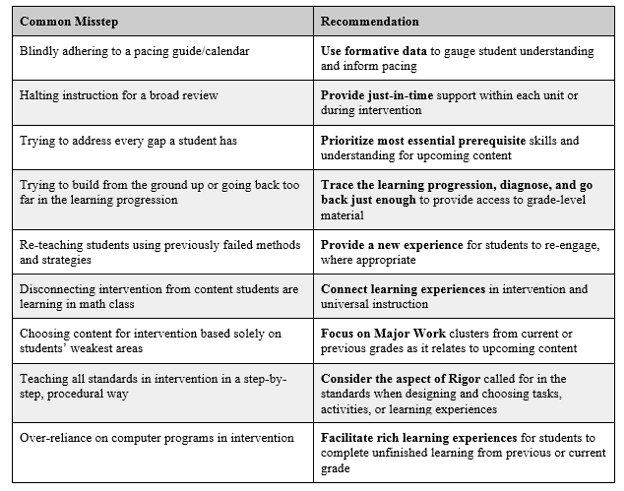
Recommendations for Targeted Math and Intervention
Evidence of the Shifts in Mathematics are found in the Recommendations for Targeted Math and Intervention chart. When teachers plan universal instruction with Focus, Coherence, and Rigor in mind, but ignore these Shifts when it comes to intervention and support time, there is an immediate disconnect in instruction. The Shifts must be top of mind for both whole-class instruction and extra support. Let’s break a few of these down.
With Focus, intervention time should be based on the content that matters most for success in later mathematics. For instance, if a third grade student’s interim data illustrates weaknesses in two clusters: 3.G.A Reason with shapes and their attributes and 3. NF.A.1 Develop understanding of fractions as numbers, prioritize the fraction work since this reflects the Major Work of the Grade. Maintaining attention to Major Work of the Grade will ensure that additional time and attention is spent on foundational content necessary for students to be successful with future math work.
When planning for Coherence, use the Coherence Map to trace content across the grades and design learning activities that support grade-level mathematics. Make connections explicit to students to support their developing thinking and understanding.
Remember that the standards themselves call for particular aspects of Rigor. Teaching tricks that proceduralize concepts and make ideas “quick and easy” for students undermines learning. Stay true to the aspect of Rigor in the standard and plan as such. For example, if intervening on 6.NS.B.2, Fluently divide multi-digit numbers using the standard algorithm, teach the standard algorithm and practice, practice, practice!
The suggestions in the chart likely can’t all be tackled at one time. Determine where to start, what changes can be made, and how to move forward. It is important to consider interventions within the “big picture” of math education. This means taking a step back and applying the same principles you apply to your planning of whole-class instruction. At first, this may seem counterintuitive. It can be tempting to give in to gut reactions: “I need to address every gap, right now before I move on;” “I need to focus just on the unfinished learning—connecting grade-level content would just be confusing.” The reality is, however, that if we give in to these inclinations, we’re denying students access to grade-level content and Shifts-aligned instruction. And that isn’t fair to our students.
Where can we find guidance in selecting the “content that matters most for success in later mathematics” for our grade
Thanks for the inquiry! The simple answer is that the ‘content that matters most’ or the major work of the grades in K-8, can be found in the focus documents. When you find your grade and start to examine the math, it’s important to know that the major work clusters of each grade were not randomly selected but are based on research that the standards themselves were grounded in and mirror content taught most extensively in high performing countries. The more complex answer, is that it’s also important to consider what the student is struggling with in regards to grade-level work. So sometimes this might mean prioritizing extra support efforts on grade-level focus standards. Other times this might mean connecting content students are struggling with to content from previous grades. An additional resource that can help illustrate those connections is the Coherence Map.
While working with a 7th grade student on computations with integers, I discovered he does not know his multiplication facts. How can I intervene to help this student?
Hi Virginia,
Thanks for reaching out. Filling in those fluency gaps is important. For some expedited remediation, we’d recommend doing some of the multiplication-related fluency activities found in these grade-by-grade guides: https://achievethecore.org/page/2948/fluency-resources-for-grade-level-routines. You should be looking in grades 3-5, and you can select the grade-level based on the student’s current proficiency. You also might find this blog post from standards’ author Jason Zimba helpful: https://achievethecore.org/aligned/using-flashcards-in-math/. In this article he describes how to efficiently use flash cards to improve fluency with math facts–the key is to stop going over facts the student knows, and really hone in on the ones the student is struggling to remember.
Making sure to connect intervention to current grade level makes sense to me when students are 1-2 years behind, but what about when they are more behind than that? We have a few kids in our school who don’t qualify for IEPs but who are 2-3 years behind in grade level content.
This is definitely a concern, especially with the drastic changes these last two school years. We are going to be seeing more and more of this. I’m interested to hear some feedback on this too!
I am guilty of re-teaching students with previously used and failed strategies. Do you have a suggestion for resources for high school Math 1-2-3 … methods for re-teaching examples? I was thinking about preparing a PLC using the Shifts-Aligned Interventions. Is there a place I could find “examples” of the Common Missteps and Recommendations in a high school math class would look like?
SVMI discusses re-engagement lessons. Good examples are the MARS tasks developed by the Shell Centre et al. https://www.map.mathshell.org/
which was part of a broader effort https://www.mathshell.org/ba_mars.htm
I can see the reteaching all gaps can take away from understanding future lessons. I try to only focus on what’s essential for success. Example, multiplying small numbers in order to create equivalent fractions for fourth graders.
reteaching in order to fill in the gaps does not have to be a time consuming process. When I taught elementary this often required several targeted mini lessons with the child’s stakeholders. Quick but consistent strategies from websites, manipulatives/games, flashcards, etc. I feel the key to success is an understanding of the student’s learning modality then nearly daily follow up.
This article made me reflect on prior years and how it was stressful trying to reteach. Instead I could have provided a new experience for students to re-engage as needed. Now my focus will be to focus on rigor when designing extra practice tasks and activities using the explicit standards to guide me. Then I know I have to prioritize essential skills needed to complete the upcoming lessons.
This article make me reflect on how I was trying to plan reteaching in previous years rather than look at the big picture and apply the same principles that I applied for planning of whole class instruction. I will facilitate rich and rigorous learning experiences.
Allowing extra time to fill gaps is simply not enough. Students need past content to be presented with new content in order to create rigor and create educational progression within the classroom.
I agree with this article that over-reliance on computer based educational programs is a real thing. Some struggling schools make students spend way too much time on Iready in hopes of boosting test scores. While Iready is a great program, many students are tactile learners and need other techniques to help them learn. Also, it is not healthy to spend too much time in front of a computer screen.
I agree with my peers on most points previously mentioned. Over reliance on computers/technology is a big issue especially in the younger grades. Even talking with my high school daughter she has issues with this. Teachers not teaching and she is forced to rely on computer programs to teach her. How we plan to reteach. Looking at smaller parts where the deficit truly lies versus the bigger picture. Teaching with fidelity and rigor, etc.