In this interview, we speak with mathematics experts Grace Kelemanik and Amy Lucenta, co-founders of Fostering Math Practices. Their work focuses on fostering mathematical thinking practices in all students. In this blog post, they’ll respond to questions about how math instructional routines can specifically support students with disabilities to engage with grade-level math content and discussions.

What are some of the most common reasons students with disabilities struggle to engage with grade-level math? 

There are a myriad of reasons that students with disabilities struggle to engage in grade-level math,  ranging from perceived gaps in prerequisite concept understanding to experiencing math education in ways that don’t support their learning. In response, with good intentions, we often break down content and procedures into bite-size pieces so that students will have short-term success in a given lesson or unit. This provides students and teachers with an illusion of learning; however, students then struggle to remember the procedure and/or which procedure to apply outside of a specific context.  The illusion of learning is short-lived. 

What is missing from traditional instructional materials and/or instructional practice that makes it challenging for students with disabilities to be successful in grade-level math?

We are fond of saying, “It’s not the instructional materials, it’s what you do with them.” Of course, that’s assuming the materials are aligned to the content and practice standards! Implementing standards-aligned materials in a way that engages and supports each and every learner in meaningful mathematics means integrating specific designs that allow students to make sense of and process concepts through multimodal- and discourse-based experiences. Here are some things to consider implementing in your classes to enhance your curriculum to better support all students, including those with disabilities:

• Supporting Language Development: Language plays an essential role in concept development so students need to be doing the majority of talking in the classroom.  Instructional strategies like 4Rs –Repeat, Rephrase, Reword, and Record–and Sentence Frames and Starters support students with learning disabilities to engage in critical conversations.
  

  

   

• Creating Multiple Opportunities to Learn: It takes time and multiple passes to develop understanding, so students need regular opportunities to think about, talk through, and refine ideas with a partner.  Implementing Turn and Talks is critical to providing students such opportunities regularly.

• Showing Multiple Representations: In order to develop and solidify ideas, students need to be able to connect what they are saying and hearing to a visual representation of the mathematics, so students need multiple representations available. Annotation of visuals–either by the student or teacher–allows students to track ideas and connect language and concepts.
• Supporting Internal Sense-Making: It’s critical that students develop their own internal sense-making process to get started and to “jump start” their thinking when they get stuck. In addition to asking direct questions of students, it’s important to develop students’ capacities to ask themselves questions to foster independence and combat learned helplessness. Implementing “Ask Yourself Questions” is a high-leverage instructional strategy to orient students to the thinking without telling them how to think.

Math Instructional Routines are repeatable activity structures with consistent designs for interaction between and among students, teachers, and content. Teachers can use these routines with a variety of content at the center of them.  More specifically, Routines for Reasoning integrates essential strategies to engage each and every learner in developing critical mathematical thinking. Routines for Reasoning were developed in order to foster the Standards for MathematicalPractice in ALL students, and out of the fear that some students wouldn’t have access to the thinking articulated by Common Core State Standards. Each routine fosters a specific avenue of thinking articulated in the Standards for Mathematical Practice. Currently, there are resources for six reasoning routines at www.fosteringmathpractices.com. What are Math Instructional Routines? What can teachers find on the Fostering Math Practices Website? What goals were the routines designed to address? 

How can the routines specifically support some of the most common needs for students with disabilities?

Routines for Reasoning support students in three ways. For starters, reasoning routines integrate five essential strategies that are high-leverage supports for all learners and critical supports for students with learning disabilities: Annotation, Ask Yourself Questions, Four R’s, Sentence Frames and Starters, and Turn and Talks. As we discussed above, these strategies create learning situations to provide students opportunities to develop language, process ideas, synthesize concepts, and develop agency. 

Secondly, when students engage in instructional routines, they no longer have to think about the flow of the lesson, the directions, or how they will engage. This predictability lowers anxiety and increases comfort and engagement. Ultimately, students’ minds are freed up to do the heavy lifting of developing mathematical thinking and reasoning.  

Finally, when these routines are implemented consistently, every student can have access to grade-level mathematics and will see themselves as the mathematicians they are.  

What does this look like in practice?

Let’s take a look at an important mathematical property: the distributive property. Often, students learn to apply the property by completing problem sets and drawing arches from the factor outside the parentheses to each of the addends inside the parentheses. Yet, students still forget to apply the multiplication all the way through the parentheses. Using the Connecting Representations reasoning routine pushes against the procedural approach and presses for a structural and conceptual understanding.

You can watch the “Connections Representations: Algebra I Distributive Property” video on this page to see the routine in action.  The class will consider the following task, and the students will work to make connections between the expressions and the visual.  

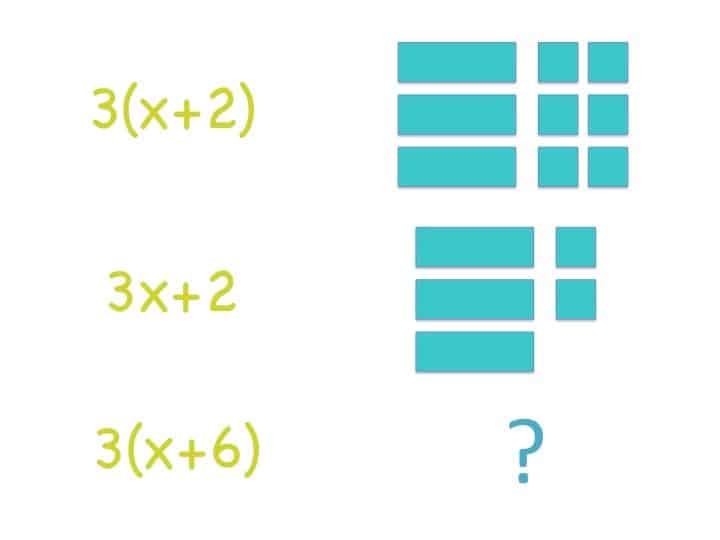
As you watch, look for how students engage, how they develop their capacity to listen to each other, and how they think and talk about the distributive property structurally and conceptually. In addition, look for the strategies we’ve named (Annotation, Ask Yourself Questions, Four R’s, Sentence Frames and Starters, and Turn and Talks) and how they support the development of students’ understanding.