In my last posts we explored the Most Misunderstood Middle School Mathematics Standards in Grade 6 and Grade 7. I have loved the conversations I’ve engaged in with math educators about the posts and welcome more people to let me know your thoughts! I can be found on Twitter here: @FLMathNinja.
In this post, we are going to dive into the most misunderstood middle school standards in Grade 8. Again, this is not about evaluating or judging teachers, but looking at the practice of mathematics instruction in Grade 8 holistically, and learning more together about the standards. With that said, these are not the only misunderstood standards, but are those that I have seen the most over the years while supporting teachers.
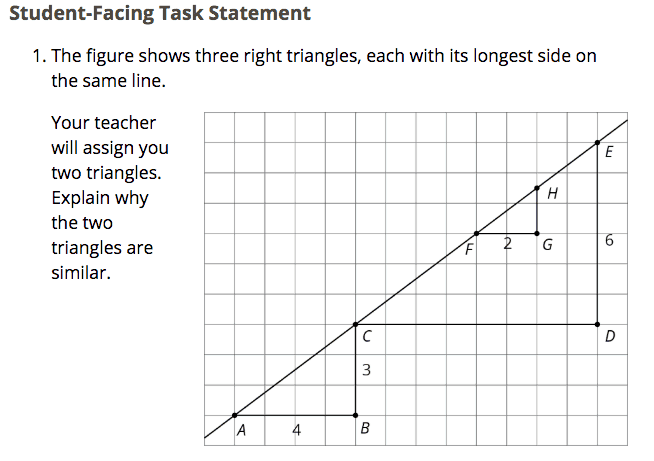
I would like to go more in-depth with three of these Grade 8 Standards, starting with 8.EE.B.6, Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y = mx for a line through the origin and the equation y = mx + b for a line intercepting the vertical axis at b.
When thinking about the aspect of Rigor to be emphasized during instruction, teachers should consider this very much a conceptual standard. In my experience of classroom observations and instructional coaching, sometimes instruction for this standard leads with the procedure of calculating slope using the formula, which strips students of the opportunity to make sense of the meaning of slope and the strong connection it has to their work with Ratio and Proportional Reasoning in grade 7 and transformations in 8.G.A.
In this lesson from Open Up Resources, students are asked to explain why their two assigned triangles are similar. One goal of this lesson is for students to realize no matter how they construct a right triangle with a line segment on line AE as the hypotenuse, they will obtain a constant ratio (when dividing the vertical distance by the horizontal distance). After this key discovery by the students, the teacher can set up the conditions to engage students in Math Practice 8: Look for and express regularity in repeated reasoning. Through repeated calculations of determining the slope using similar triangles, the students will be able to make sense of the standard formula for slope and use it as an alternative method for determining slope.
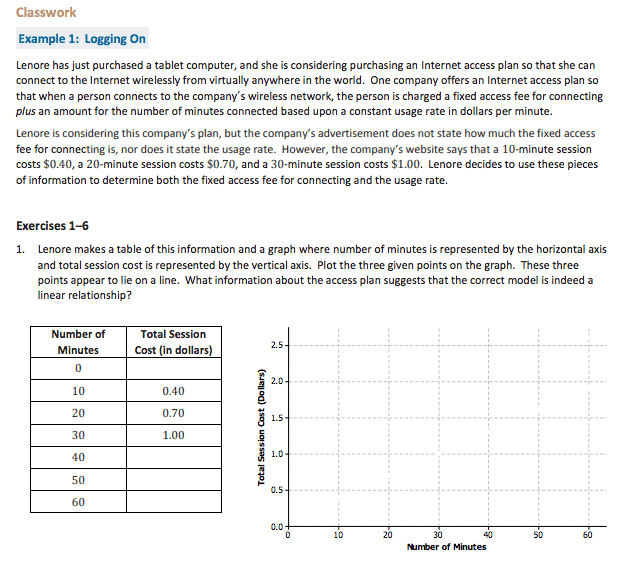
The next standard I would like to discuss is 8.F.B.4, Construct a function to model a linear relationship between two quantities. Determine the rate of change and initial value of the function from a description of a relationship or from two (x, y) values, including reading these from a table or from a graph. Interpret the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
For whatever reason, instruction seems to be limited to constructing the function only and does not focus on interpreting the rate of change and initial value of a linear function in terms of the situation it models, and in terms of its graph or a table of values.
In this lesson by EngageNY, students have to not only construct the function to model the situation, but they must also interpret the rate of change and the initial value within the context. The openness of the problem (Exercises 1-6) allows students to use their prior understanding from the Expression and Equations Domain to engage in this task using multiple representations (table, graph, function, verbal description).
According to the Focus by Grade Level, Geometry does not show up as Major Work in Middle School until Grade 8. With that in mind, I would like to address the last standard from the Geometry Domain, 8.G.B.7: Apply the Pythagorean Theorem to determine unknown side lengths in right triangles in real-world and mathematical problems in two and three dimensions. In my experience in classrooms, instruction typically is limited to two dimensions and does not extend the Pythagorean Theorem to three dimensions.
Here is a nice task in the Grade 8 Curriculum from Open Up Resources that gets at what students are expected to be able to do when applying the Pythagorean Theorem in three dimensions. Students need to use the Pythagorean Theorem twice in this context: once for finding the length of the hypotenuse of the triangle created by the base, which in turn becomes a leg of the second right triangle used to find the length of the blue diagonal. Using a two-dimensional drawing of a three-dimensional figure can be difficult for some students to visualize, so be sure to have physical models of the rectangular prisms handy as students grapple with this task!
As I said in my last post, the suggestions given here are just a start to figuring out this very challenging profession of teaching mathematics. I hope my experiences in many middle school classrooms will help grow your brain around these standards and, now that you know better, you will do better in ensuring each student learns math at a high level. Continue to #InstructUP!



















8.G.B. Applying the Pythagorean Theorem to find distance could easily be the most challenging of all.
8.G.B Applying the Pythagorean Theorem to find distance. Enter Barbie Zipline. How would you construct a safe, yet fun zipline for Barbie if you knew that she would start her adventure 30 feet above the ground?
So, tell me how to develop students’ understanding of all these standards in time for the high-stakes test that administration and the state use to judge me, the students, and the entire school.
I long to teach for deep, true understanding, but I’m forced to play the testing game.
I think it’s time we all stop playing the “rush through content to the test” game that both gives us an excuse and does not exist. Yes, people examine data. Yes, decisions get made based on test scores. BUT, in 30 years of education, not one single time has someone come into my classroom to even discuss, much less consequence me, for not ‘teaching a topic’.
We need to create thinkers and problem solver who persevere in their tasks. Then it won’t matter if we haven’t ‘taught by telling’ them a topic (which they will not remember and will subsequently fail on the test anyway). If we make them courageous in their attempts, they will improve as mathematicians. The scores will rise accordingly.
Could you elaborate on what you mean by “instruction using functions and equations language interchangeably.”