Within the teaching profession, there is a lot demanded on a daily basis to ensure best instructional practices are being followed and student learning is being maximized. In an effort to meet these demands, teachers focus their time on the grade level and students at hand. Furthermore, some teachers admit to even just grazing over strategies with students when they were too challenging or when teachers did not see the benefit. This hinders the understanding and beneficial discussions that should be taking place around the vertical progression of math learning. The Math Milestones™ tasks provided our teachers with a wonderful opportunity this year to dig deeply into student learning across the grade bands while reviewing our students’ learning and understanding through the tasks.
Over the course of a year, teachers in first through eighth grades had the opportunity to utilize the different grade-level math tasks with their students. More importantly, they then worked as a grades 1-8 professional learning community to dive into the math strategies that were specifically being used by students to solve these tasks. This opportunity facilitated discussions around how strategies progressed through the grade levels and facilitated math learning through addition and subtraction to multiplication to solving equations. Many teachers are used to following the adopted curriculum, which does not always align directly to the grade-level standards. For instance, the fourth-grade task involving multiplication and division allowed for a deeper discussion on area model as a strategy without introducing students to the standard algorithm, which also gave additional time for students to master one strategy rather than having to tackle multiple strategies. Additionally, the discussions that took place vertically built a stronger understanding of the reason certain strategies to be continually utilized throughout the grade levels. The middle school teachers were able to understand how a fourth-grade area model was not only utilized within multiplication but also in division, and they gained a deeper understanding of what background knowledge students would be coming into their classrooms having. The first-grade teachers gained a deeper understanding of the importance of students having a strong ability in doing ten more or ten less and what this meant in regards to place value. These discussions were extremely beneficial, especially as the teachers learned the updates within the Wisconsin Standards for Mathematics and the switch in grade-level focus.
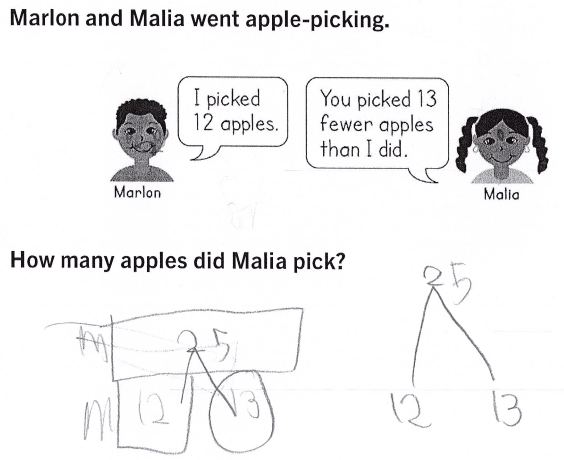
Additionally, each grade level expressed a need for a strategy to be taught, such as comparative bars, in order to facilitate future learning. The second-grade task 2:13 (see image below) Apple Picking asks students to compare a whole and a part. In demonstrating both the strategy of comparative bars and “math mountain” (number bonds), the student was able to represent the problem and then find the unknown. A student who has mastered this strategy could then utilize the same strategy of comparative bars as the learning progresses into fourth grade with fractions. In utilizing the Math Milestones™ as professional development focused around vertical progression, these conversations allowed teachers to make connections with strategies and also understand what skills students came into a grade-level having been exposed to. Without the Math Milestones™ tasks and the opportunity to have these vertical progression discussions, teachers would not have the same understanding of the importance of grade-level content.
The other large focus within the Math Milestones™ tasks and the vertical progression was staff being able to recognize the areas of strength and areas of growth within students’ learning by examining the strategies utilized and errors made within. In having a fourth-grade teacher look over a sixth-grade student’s tasks, the teacher was able to provide insight on a missed learning opportunity from fourth grade that was hindering this student from mastering the sixth-grade skill. Within the discussions, there was minimal instruction given to lead the conversation beyond two questions: 1. What are the students’ strengths or areas of concern? 2. How does the learning you see connect with your grade-level instruction? Oftentimes, we unfortunately focus on the answer and not the process, missing these professional learning opportunities and chances to meet students’ needs.
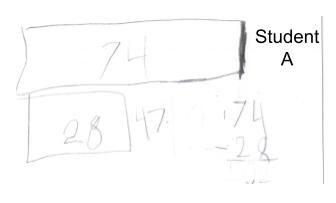
From there, teachers were able to look at what instruction should take place next to progress towards grade-level learning. As a district, we are working hard to implement small-group-based instruction to provide individual learning opportunities. Teachers utilized the work from the Math Milestones™ tasks when making these groupings and determining focus. For instance, when reviewing work on second-grade task 2:11, a teacher may look at student A’s work and determine the strategy is in place but there was an error in the math calculation. Student B’s work shows a wide array of strategies in the math tool box, but that student may have a different understanding of the question being asked in the task. When seeing the work of these students, a teacher may have grouped them together since both answered the problem incorrectly. For additional guidance, teachers looked at the Coherence Map to determine previously taught or upcoming standards that would continue the learning of all students. Those who had mastered their learning had the same opportunities within the individual setting to continue the learning, which led to even more growth in students’ math confidence. Without the vertical discussions, however, teachers may stop at proficiency or focus on reteaching the grade-level skill instead of going back to the root cause.
Over the course of this year, working with the staff on the implementation and review of the student work on the Math Milestones™ tasks created much-needed discussion around students’ math strategies and the importance of these strategies throughout the progression of their learning. It expanded the teachers’ understanding of how a strategy progressed and also how it allowed students to dive into more complex skills as they began multiplication or moved into algebraic thinking. The professional learning experience gained will lead to continued discussions next year around students’ strengths and deficits as we work to strengthen the overall math instruction at our school.


















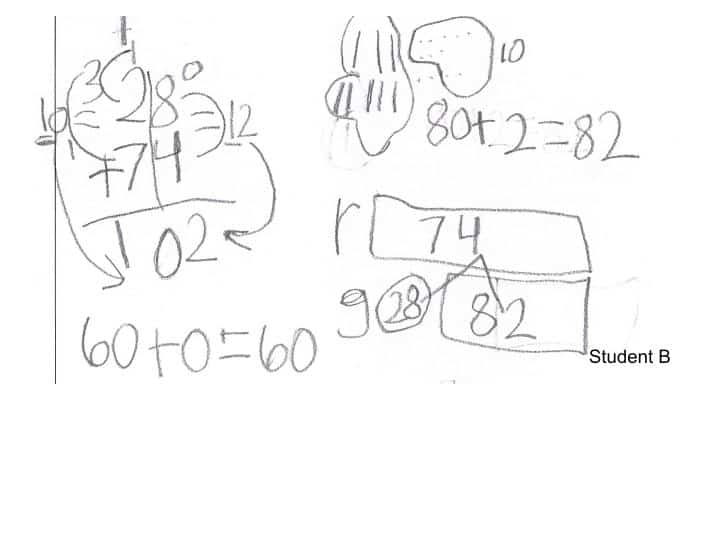
Is there a chart that shows the progression from K-5 that is based on specific domains? Thank you!