The Standards’ focus on arithmetic can allow greater variety in the tasks students see, giving students time to synthesize their developing knowledge and practice their calculation skills to fluency. One important place to have variety is in the addition and subtraction situations that students see in word problems. The case of addition and subtraction word problems reflects the general truth that there’s more to arithmetic than initially meets the eye.
Word problems can help teach students the meanings of addition, the meanings of subtraction, and the relationship of addition to subtraction. When my own kids were in the primary grades, I gave them addition and subtraction word problems. Here’s one of the worksheets I created for them back then:
As you can see, the worksheet touches on all three aspects of Rigor: procedural skill and fluency, conceptual questions, and word problems/application. Today, what I’m focusing on is the pair of word problems near the middle of the worksheet.
Let’s look at the first one:
There are 12 red apples and 2 green apples.
How many apples in all?
The situation in this problem can be described as “put together with result unknown.” Two given quantities, initially separate, are being joined, and we need the total. Over time, my daughter had gotten pretty good at questions like these; they became routine for her. Then she saw the second problem:
Candace stole 1 coin from Ferb.
Then Ferb only had 7 coins.
How many did he have at first?
I observed her as she read the words. As she began to understand what the problem was asking, she became agitated. She flatly denied that it was possible to solve this problem. She even drew a line through it!
All of this was understandable. Until then, she’d been fed a diet of result-unknown problems. This time, she was dealing with a more algebraic type of problem, a “start-unknown” problem.
It was a profound learning moment. How could I get her over the hurdle?
The way we handled it that day was with pennies. I helped her begin to represent the situation physically, and right away it became clear what the answer had to be (and that the answer could be found in the first place).
From that day onward, I began including start-unknown, change-unknown, and similarly sophisticated situation types on the worksheets—always coordinating the specific numbers in the problem to her growing skill in calculation. For example, I usually paired harder calculations with simpler situation types, and I tended to limit the harder situation types to the fact-families she already knew from memory. For harder situation types with larger numbers, we stopped using pennies or tallies to represent the situation as quickly as possible, graduating instead to modeling the problems by writing addition and subtraction equations with a question mark for the unknown quantity.
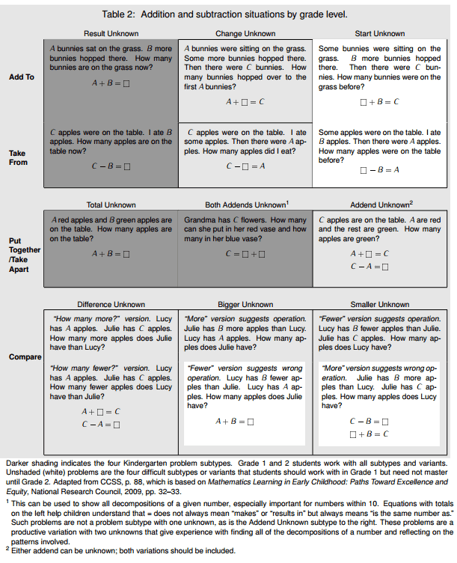
How did I know about all of these different kinds of addition and subtraction problems? I used Table 2 on page 9 of the Counting and Cardinality and Operations and Algebraic Thinking Progression Document.
The table can help ensure that lessons, unit assessments, and cumulative assessments are covering the full range of situation types. (See also this mini-assessment from Achieve the Core.)
By the way, the table of situation types isn’t meant to be a classroom poster! Students don’t need to be aware of this taxonomy. Certainly, I never said to my daughter anything along the lines of, “Today we are going to work on change-unknown problems! And here is the method that you must remember to use whenever you see one of these problems.” Instead, what I did was to choose my moments to introduce the different situations into the ongoing stream of their work, giving support at the time and plenty of practice afterwards with the full variety.
Ask a passing pedestrian to write down a word problem in addition, and you’ll probably get a situation of “Add To with Result Unknown.” Ask for a word problem in subtraction, and you’ll probably get a situation of “Take From with Result Unknown.” Those are key cases of course, but students need to work with more situations than just those, if they’re going to learn well what addition and subtraction mean. I’ve seen textbooks in the elementary grades that rarely present certain situation types; that means they aren’t fully teaching about the operations themselves. This can leave students unprepared for later grades, especially in algebra, where modeling with variables depends on students having a strong sense of what operations do.
For classroom educators in grades K-2, I recommend comparing the word problems in your curriculum to the situation types in Table 2 from the Progression document, and supplementing as necessary to ensure your students are working with the full variety of situation types for addition and subtraction. Note the shading in Table 2, which gives guidance about grade-level appropriateness of the situation types.
For publishers, I recommend using Table 2 from the Progression document to ensure that instructional materials across grades K-2 are attending to the full variety of situation types for addition and subtraction, and in the process giving students a full conception of what these operations do and how they relate to one another.
Further Reading: Progression document for Counting and Cardinality and Operations and Algebraic Thinking


















What I understand from each reading is that each grade as we already know have a level of complexity, in kindergarten we must focus on the preparations between numbers 1-5 or up to 10, using finger representation, drawings, concrete material and giving the Different students showcase their work and also share it based on the corresponding grade standards.
One thought I had was just how valuable manipulative are in math. The author’s daughter became frustrated when she couldn’t solve the word problem, but using something tangible she was able to make meaning of what was being asked. I teach kindergarten and it’s always interesting to see the connection students make when they have a visual representation.