“How far back is too far?”
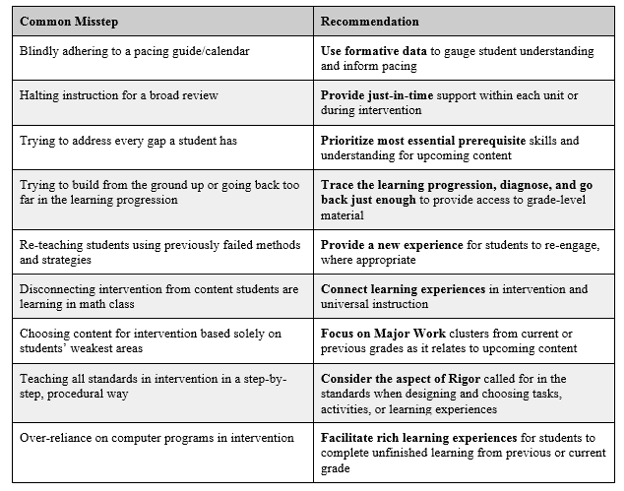
When discussing how to support mathematical learning for struggling students, this is a question I hear frequently. Of course, as with most things in education, there isn’t a simple and straightforward answer to “How far should interventions flow back in order to access grade-level content?” In a recent blog post, I addressed unfinished learning in the mathematics classroom and included this Do’s and Don’ts Chart showing some common missteps and recommendations for how to avoid them.
Since then, questions have surfaced about what it actually takes in the day-to-day bustle of instruction to enact these recommendations. Simply put, how do the recommendations come to life in the classroom? And maybe more importantly, how do they really help our most struggling learners?
First, as educators, we all know that each student is different; effective intervention is created and instructional decisions are made in the quickest flash of a day as we determine the changing needs of each student. All that to say, the chart is meant to be a beginning guide—a place to begin a discussion. So let’s break down one of the missteps and its recommendation now: In her Aligned post, Chrissy Allison shared an approach to address unfinished learning that can be applied when reaching back in progressions to address unfinished learning. Of course, the trick is going back to the “right” content.
In her Aligned post, Chrissy Allison shared an approach to address unfinished learning that can be applied when reaching back in progressions to address unfinished learning. Of course, the trick is going back to the “right” content.
Let’s try walking through an example of how we might design an intervention that goes back the appropriate amount in the learning progression. We’re going to start with the “Understand” box. In planning for an upcoming unit on fraction multiplication, a fourth grade teacher digs into the standards. Some students struggled with the fraction work that came earlier in the year around equivalence and ordering. Others struggled with the operations of adding and subtracting. He anticipates that these same students, and maybe more, may have a hard time with multiplying a fraction by a whole number (4.NF.B.4). Where to start? What to do?
Spend some time digging into student work and digging into the standards.
- In the Coherence Map, pull up the standard in question. (Make sure you can see grade 2 standards boxes.) It’s likely that there are silent shrieks echoing across American classrooms when you see that a standard maps to so much pre-requisite work. Likely this fourth grade teacher is saying, “Oh boy, do I really have to re-teach grade 2 standards to my fourth grade class so they’re successful with the fraction work?”
- Now it’s time to zero-in on the real source of the lack of understanding: the”Diagnose” step in the process pictured above. While it’s always a good decision to build in opportunities to strengthen understanding during universal instruction and reinforce the content in other units throughout the year, this may not be enough for all students. For these struggling students, find out what they know about the concept, (in this case, fractions) first. Start with the closest connection in the Coherence Map: the same domain and then consider branching farther to find the missing link. When adults say they were “bad” at math, or they just “didn’t get it,” the root causes almost always stem from a weak understanding of underlying mathematical concepts. That’s why, in this example, it’s important to assess whether the students understand fractions as numbers by first going to the conceptual underpinning of current work, or the connection within the same domain.
- Lastly, you need to actually plan the targeted intervention once you’ve narrowed the cause of the knowledge gap. Unfinished learning around the 4.NF.B.4 standard is a tough nut to crack since the conceptual foundation could pull from grade 3 fractions, 3.NF.A.1, or the meaning of multiplication in 3.OA.A.1. It is always hard to hear something like “it could be this, or it could be that,”but flexibility and listening and observing the students are important factors here since the teacher should be prepared to take an alternate path if needed. The teacher first draws on the 3.NF connection and if the understanding is secure with fractions, moves to the 3.OA connection to take action on unfinished learning on the meaning of multiplication. The Coherence Map has sample tasks and assessment items to help you get started with your intervention.
Our students’ time, and our own time as educators, is incredibly valuable. Our job as math instructors is to help our struggling students plug the gaps, as quickly as possible, that are precluding them from accessing grade-level content. The longer they are not accessing grade-level content, the farther behind they will fall, leaving it in question whether they can stay on pace for the next year’s learning/content and to eventually leave high school ready for college and their careers. While it may be tempting to start from square one with our interventions, our students don’t have time to re-take 2nd grade math in 4th grade—and they don’t need to. Strategic intervention planning helps us, and our students, tackle gaps more quickly. When students see themselves as incapable of doing the grade-level work their peers are doing, the more likely they are to convince themselves they “aren’t math people,” so our efficient interventions are critical now.




















I’m wondering whether moving ALL students at grade level is realistic? The normal spread between those well ahead (of grade level) and well behind runs to at least 3 grade levels by 3rd grade and more by 6th.
With better methods the lower-end tail might be reduced. Should the higher end individuals be suppressed?
The understand-diagnose-take action approach and examples mentioned in the blog are meant to illustrate possible intervention strategies for students struggling with grade level content. Multi-tiered system of support (MTSS) includes gifted students, but this blog does not include examples or instructional practices that were meant to support students performing well above grade level.
Is this considered researched based? I am looking for something to implement in my Title One Math groups in the State of Ohio but am told that it has to be research based.
I have the same question. Is this researched-based? If so, can you direct me to the research so I can further look into how to select math intervention content?
Thank you!
Help me with how to do this with high school. The coherence map does not include high school standards.
It will soon, Andrea! The HS standards will be part of the Coherence Map in just a few weeks. Keep an eye on your email/Twitter or wherever you learn about new content from Achieve the Core.
Yes, I also need research-based resources for intervention, in particular grade 5 place value with decimals including rounding and comparing
The understand-diagnose-take action approach is great to use as an intervention strategy for struggling students with grade level content. The learning acceleration approach makes sense and I can’t wait to be use in our classrooms.
I agree with strategic intervention however some students are more willing to work on their educational gaps than others. I tell students I am readily available however not all students take advantage of their teachers availability to help.