I’m often asked, if I were designing an intervention program at a school or in a classroom, where I would start. The question usually becomes a conversation in which the Recommendations chart in this blog post is mentioned. People often ask, “Are the rows listed in order?” Followed quickly again by, “Where should we start?” To be honest, I haven’t had much of an answer up until this point. Intervention is student-based; paths can vary depending on content needs, and school systems and structures are set up in so many variations that the trajectory of an intervention strategy really varies by situation. However, I’ve recently landed at a “start-here-at-square-one” suggestion and it’s content-based–go figure!
In order to help our struggling learners with gaps and misunderstandings, we want to establish supports around high-impact actions that lead to deepening understanding and mastery of grade-level content. Grade-level content and connections to grade-level content need to be where we start. I believe this means thinking about what it is students are expected to know, understand, and be able to do at grade level, and then prioritize based on that.
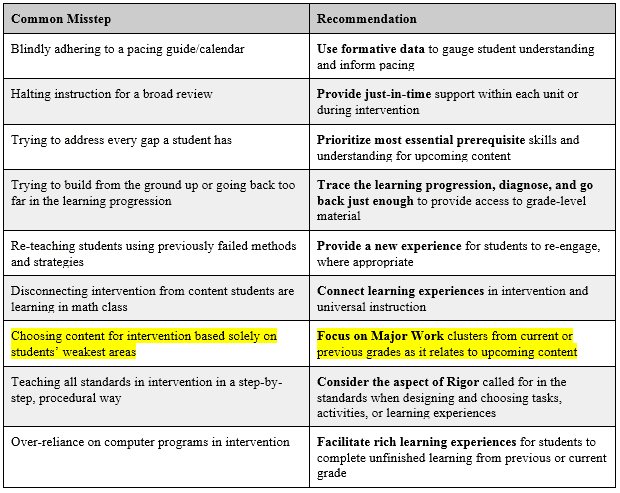
Prioritizing standards kicks off an investigation into the content most needed for success in later mathematics. The Focus By Grade Level documents are just the resources to analyze and plan with as the intervention paths are set in motion. Therefore, the first step is actually the seventh listed recommendation on the chart!
In selecting Major Work clusters on grade level or from future grades, educators are helping to build understanding in the most essential mathematical content needed for success in algebra and beyond. It seems fundamental that interventions focus on the most important content, but I’ve witnessed far too many interventions spent on Additional content of the grade or grades below. Selecting interventions in Major Work–over Additional content clusters– is an important first step in prioritizing an educational plan leading to more meaningful understanding of mathematics.
Skeptics might push on this and accuse me of minimizing some grade-level expectations. I guess that’s true, I am. In minimizing some content and prioritizing other content all holes might not get filled (to use the proverbial bucket analogy). But knowing we have very limited time to get students working on grade level, why not start with the content that connects to the most important grade-level concepts–the concepts that have the most potential to help serve students in the long run?
Seventh grade students struggling with multiplying and dividing fractions shouldn’t spend their intervention block investigating probability even if probability was their weakest reporting category on a benchmark assessment. They should have their intervention block focus on the Major Work from grade 6 and possibly below. (The Coherence Map can help you see where the unfinished Major Work likely is.) This is what will give students access to grade 7 math content and beyond. Furthermore, the intervention on fraction operations doesn’t need to be situated outside of grade-level work; it should occur in conjunction with universal instruction in grade 7 units on the Number System and/or Expressions and Equations.
The same is true of other Major Work concepts which can be seamlessly addressed alongside grade-level learning. By aligning the below-grade-level intervention to the most tightly connected on-grade-level content, coherence can be strengthened between what students know and what they are learning. The strongest intervention systems prioritize and bridge content in meaningful ways, allowing students the opportunities to build connections and make meaning of the mathematics. The outcome? Learning!
This is not an easy task and there’s lots of thoughtful planning on this journey. Hopefully the series of posts, the resources mentioned, and the Coherence Map can help with the first step: Focusing on Major Work clusters from current or previous grades as it relates to upcoming content. Take the first step! It can make a big impact in designing math interventions to support learners.



















We need to study our students; knowing what they like the most can help us to teach them the fundamental concepts of arithmetic. And like learning a foreign language when we have learned enough vocabularies, it is most beneficial to use them to read a page of an easy reading book. It is the same way with arithmetic: the students need to be fluent in reading arithmetic sentences in the areas that they are interested in; they can relate their fluency in arithmetic with their interest. This way, they never forget the fundamental concepts and they can build on the fundamentals to learn more advance operations and eventually use them in their adulthood and appreciate arithmetic and mathematics !
The most powerful statements for me…By aligning the below-grade-level intervention to the most tightly connected on-grade-level content, coherence can be strengthened between what students know and what they are learning. The strongest intervention systems prioritize and bridge content in meaningful ways, allowing students the opportunities to build connections and make meaning of the mathematics. The outcome? Learning!
My concern with the “Focus on Major Work” is students being unable to differentiate the new content from the old content. I’ve noticed student using old techniques for the new content being taught and it does not correlate.