
-
- 02/25/15 | Adjusted: 08/01/18 | 2 files
- Grades 5
- 02/25/15 | Adjusted: 08/01/18 | 2 files
Sharing Chocolate ©
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: 5.NF.A, 5.NF.B.3, and 4.NF.B.3d
- Provides opportunity to use concrete representation (pictures or sketches of chocolate bars or actual bars of chocolate) to model the mathematics for 5.NF.B.3
- Allows for varied solution methods that lead to correct answers
- Connects to adding fractions with unlike denominators (5.NF.A)
- Expands on comparing and adding fractions with like denominators (4.NF.A, 4.NF.B.3d)
In the classroom:
- Includes discussion questions that prompt students to share their developing thinking and assist teacher in checking for understanding
- Facilitates using a variety of solution methods and representations to strengthen the understanding of all students
- Allows for small group, partner, or individual work
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Elicits evidence of student thinking both verbally and in written form.
- Includes a mathematical routine that reflects best practices to supporting English Language Learners in accessing mathematical concepts.
- Offers the opportunity for students to act out the problem when the task features complex real-world situations.
-
Making the Shifts
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the major work of fifth grade Coherence Revisits students' understanding of fraction equivalence and comparison, and builds on adding fractions with like denominators Rigor Conceptual Understanding: primary in this task
Procedural Skill and Fluency: not targeted in this task
Application: primary in this task
-
Task
Task: Problem Scenario
Two groups of friends are sharing chocolate bars. Each group wants to share the chocolate bars fairly so that every person gets the same amount and no chocolate remains.
In the first group of friends, four students receive three chocolate bars. How much chocolate did each person get? In the second group of friends, eight students are given six chocolate bars. How much chocolate did each person get? Which group of students got more chocolate?
Task: Classroom Setup
Before presenting the problem to your students, you will need to gather some materials:
- A large piece of paper for each pair or group of students to record their solutions
- Pens or markers
- Pictures or sketches of the chocolate bars and students for both situations (three chocolate bars and four friends, six chocolate bars and eight friends)
- Copies of a blackline master with equal-size rectangles (eight rectangles to a page)
- A digital camera, a smartphone, or a tablet with a camera
-
Where's the Math?
In this problem, to share the chocolate bars equally in a situation where there are fewer bars than people, students will need to divide a "whole" into fractional amounts. This problem scenario encourages students to think of fractions to represent the division of the chocolate into equal amounts and could lead students to generalize that the fraction would represent the number of chocolate bars divided by the number of people. It also may cause students to think about defining the "whole" in situations involving fractions. Because the questions asks how much chocolate each person will get, some students may provide the answer with the fractional amount three-fourths, using one chocolate bar as the whole. Another student may consider all three chocolate bars as the whole and provide an answer of three-twelfths. Both answers could be correct, depending on the definition of the whole.
The problem also provides opportunities for discussing the meaning and creation of equivalent fractions, such as one-half plus one-fourth being equal to three-fourths or by determining that three-fourths can be changed into six-eighths by dividing each fourth in half.
-
Discussion & Follow-Up Questions
Teachers and those who support teachers may find the Instructional Practice Guide: Coaching Tool useful in implementing best practices in the classroom that allow all students to master the content of the lesson.
To promote student thinking:
- Which group are you thinking about?
- How many chocolate bars does this group have? How many students?
- How could you share the chocolate equally?
- Do you think each person will get more or less than one chocolate bar?
- What does the 3 mean: three what?
- So how much chocolate does each person get?
- How could you find out which group of students got more chocolate?
To prompt discussion:
- Do you have any questions about this solution?
- Which answer is correct?
- Is one-half and one-fourth of a chocolate bar the same as three-fourths of a chocolate bar? How do you know?
- Which is right, three-fourths or three-twelfths?
For follow up:
- Who things group 2 got more chocolate? Why?
- Who disagrees? Why?
- If group 2 got six pieces, isn’t that more than group 1, because it got three pieces?
- How can three-fourths be the same as six-eighths?
-
Extensions and Modifications
For students who finish early, provide a third scenario: a group of five friends who have four chocolate bars. Ask students to determine how much chocolate this group would get and to find out if it is equal to the other groups.
Because this activity contains three questions, it has built-in opportunities for differentiation. Some students may be able to provide an answer for only the first question. Others may be able to solve the first two questions but not the third, which asks them to compare the amounts. These students can still participate in solving the problems and in the resulting discussions.
-
Solutions & Sample Work
Solutions:
The solutions to the three parts are:
- Fractions equivalent to $\frac{3}{4}$.*
- Fractions equivalent to $\frac{6}{8}$.*
- A statement that the groups received the same amount of chocolate for each person in the group.
*If the student considers all the chocolate to be the whole, then fractions equivalent to $\frac{3}{12}$ would be correct for the first part and fractions equivalent to $\frac{6}{48}$ would be correct for the second part (See Where's the Math for more information.). But these students would need to do more reasoning to compare the amount of chocolate each person received.
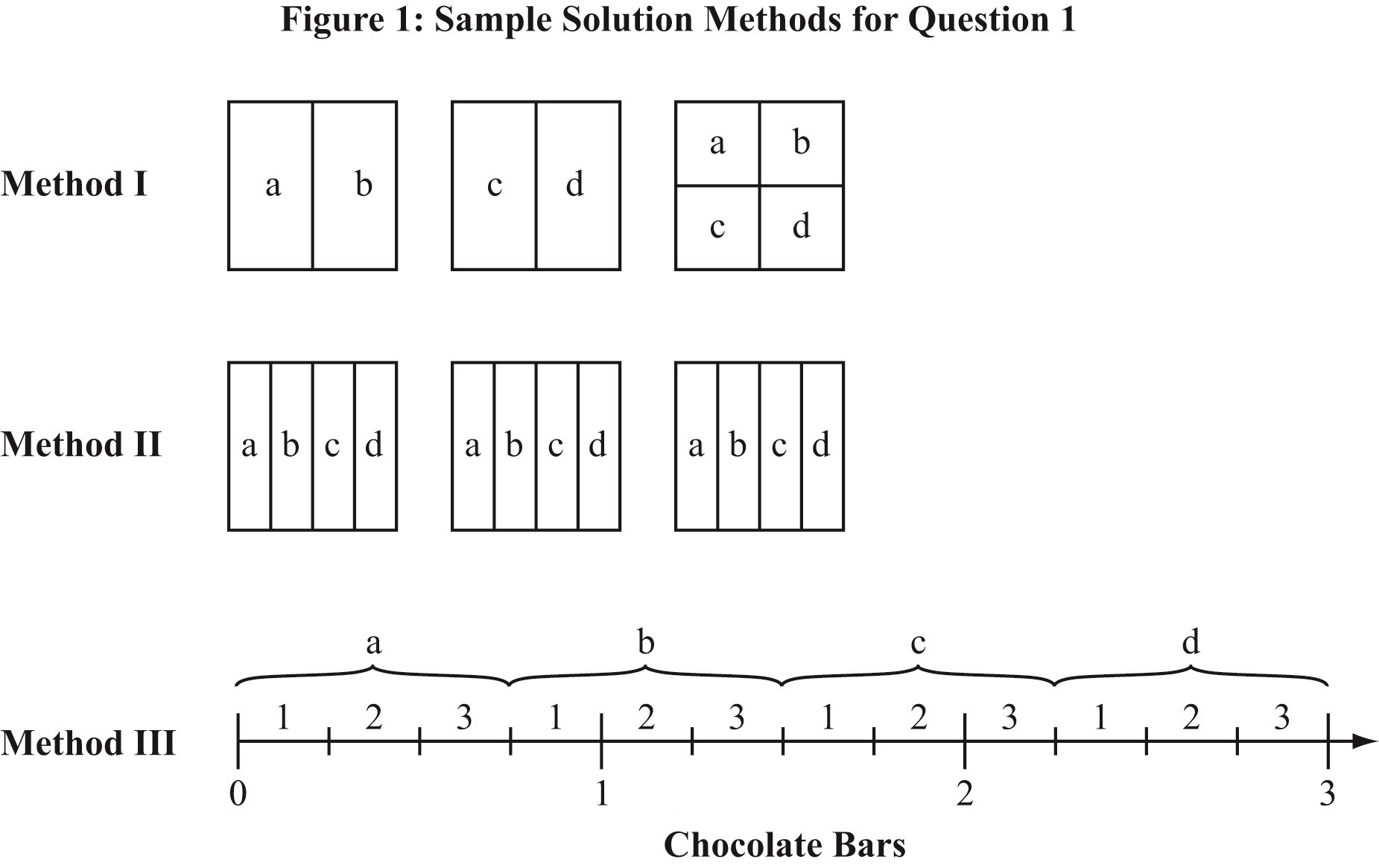
Sample Work:
Sample work may include:
- For the first part:
- Using method I: Each person gets $\frac{1}{2}+\frac{1}{4}$ (or $\frac{3}{4}$) chocolate bar.
- Using method II: Each person gets $\frac{1}{4}+\frac{1}{4}+\frac{1}{4}$ (or $\frac{3}{4}$) chocolate bar.
- Using method III: Each person gets 3 parts of a whole bar broken into 4 parts (or $\frac{3}{4}$).
- For the second part:
- Using method I: Each person gets $\frac{1}{2}$ chocolate bar which leaves 2 whole chocolate bars remaining. Then the 8 friends divide those chocolate bars into quarters so that they each get an equal share. So, each person gets $\frac{1}{2}+\frac{1}{4}$ (or $\frac{3}{4}$) chocolate bar.
- Using method II: Each of the 6 chocolate bars is divided into eighths, with each of the 8 friends taking one piece from each bar. So, each person gets $\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}$ (or $\frac{6}{8}$) chocolate bar.
- Using method III: Each person gets 6 parts of a whole bar broken into 8 parts (or $\frac{6}{8}$).
- Correct reasoning comparing the two amounts:
- "I know that $\frac{3}{4}$ and $\frac{6}{8}$ are equivalent because $\frac{3}{4}×\frac{2}{2}=\frac{6}{8}$."
- "I made a model using one chocolate bar as a whole. Then, I created an area model of $\frac{3}{4}$ and $\frac{6}{8}$. The two models showed the same amount."
- "I made a number line and put both numbers on it. They were at the same location on the number line so I knew they were the same amounts."
-
Additional Thoughts
This task offers students an opportunity to think about dividing whole numbers in a variety of ways. Whichever method a student chooses, the key is that students understand and interpret a fraction as division of the numerator (the number of chocolate bars) by the denominator (the number of people). In order to make this connection explicit, students need time to think about how the solutions for problems 1 and 2 relate back to the division required (e.g., how $\frac{3}{4}$ relates back to the original 3 chocolate bars shared equally by 4 students). Teachers could then show students another fraction (e.g., $\frac{2}{5}$) and ask, “If 5 students were sharing chocolate bars equally and each received 2/5 of a bar, how many chocolate bars were there to begin?”
For more insight on dividing fractions concepts in grade 5, read pages 11 and 12 of the progression document, 3–5 Number and Operations – Fractions.