• Making the Shifts
• a. Students follow these steps with the fraction cards:

  This activity is designed for pairs of students. It uses a set of cards and a fraction mat which are supplied as an attached resource, after the commentary . The goal is to place each fraction in the appropriate category on the mat. Instructions for the activity are as follows:

  a. Students follow these steps with the fraction cards:

  1. Each student in the pair select a card.
  2. Student 1 places his/her card within the appropriate category on the mat and gives an explanation for the placement.
  3. Student 2 either agrees or disagrees with the placement.
  4. If the partners disagree, they discuss until reaching a consensus.
  5. If the partners agree, Student 2 places his/her card and repeat steps 1 through 4 with this card.

  b. After 5 rounds, each pair record observations about what methods they used to categorize the fractions.

• Two different sets of cards are provided as attachments, one with a picture of the fractions being compared and one without. The pictures allow students to make a visual comparison of the fractions which is important. However, the teacher may wish for students to use a different method of comparison or to provide these pictures as they explain their decision. Some of the pictures such as those of $\frac{1}{3}$ and $\frac{2}{6}$, are not designed to visually demonstrate equivalence so the cards with pictures will still help develop non visual understanding of fractions.

  Commentary

  The goal of this task is to determine appropriate benchmarks for fractions with a focus on providing explanations that demonstrate deep conceptual understanding. The only benchmark fractions addressed in this task are $\frac{1}{2}$ and 1. Some important ideas to look and listen for as the students work are

  • A fraction is bigger than one if the numerator is larger than the denominator (e.g. $\frac{7}{6}$) and a fraction is less than one if the numerator is smaller than the denominator (e.g. $\frac{2}{5}$). A fraction is equal to one if the numerator is equal to the denominator (e.g. $\frac{3}{3}$).
  • A fraction is bigger than $\frac{1}{2}$ if the denominator is less than two times the numerator. A fraction is equal to $\frac{1}{2}$ if the denominator is equal to two times the numerator. A fraction is less than $\frac{1}{1}$ if the denominator is more than twice the numerator.
  • Students can draw pictures of fractions to compare them with $\frac{1}{2}$ and 1.
  • Students can plot fractions on the number line to compare them with $\frac{1}{2}$ and 1 (3.NF.A.2).

  Two different sets of cards are provided as attachments, one with a picture of the fractions being compared and one without. The pictures allow students to make a visual comparison of the fractions which is important. However, the teacher may wish for students to use a different method of comparison or to provide these pictures as they explain their decision. Some of the pictures such as those of $\frac{1}{3}$ and $\frac{2}{6}$, are not designed to visually demonstrate equivalence so the cards with pictures will still help develop non visual understanding of fractions.

  Differentiated fraction mats are provided as attachments to allow students to work with broader benchmark ranges. These mats can be used in progression based on student understandings. The first mat asks students to identify fractions greater than or less than 1. The second mat asks students to identify fractions equivalent to $\frac{1}{2}$ and 1. The third mat asks students to use the prior understandings of the previous mats to identify fractions that fall within the benchmarks of $\frac{1}{2}$ and 1.

  Solution 

  a. In order to place a fraction in the proper category students must compare the fraction to $\frac{1}{2}$  and 1. There are many strategies to do this and the student does not need to follow the particular order of reasoning described here:

  • Fractions whose value is equal to 1. These are perhaps the simplest fractions to recognize: for example, $\frac{8}{8}$ is equal to 1 whole because it takes 8 equal pieces of $\frac{1}{8}$ combine to create a whole.
  • Fractions equivalent to $\frac{1}{2}$. For example $\frac{2}{4}$ is equivalent to $\frac{1}{2}$ because the numerator is half of the denominator. One way to show that these fractions represent the same quantity is with a picture:

  

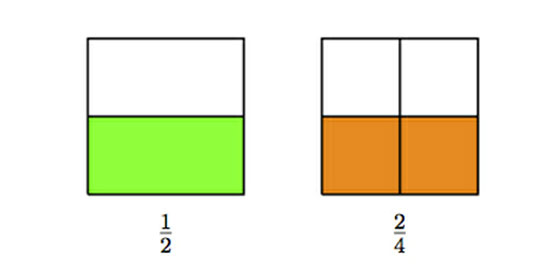
  • Fractions whose value is less than $\frac{1}{2}$. For example, $\frac{3}{8}$ is less  than $\frac{1}{2}$ because $\frac{4}{8}$ is equivalent to $\frac{1}{2}$ and $\frac{3}{8}$ is $\frac{1}{8}$ less than $\frac{1}{2}$, therefore less than $\frac{1}{2}$.
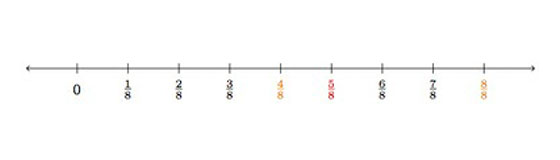
  • Fractions whose value is greater than $\frac{1}{2}$, but less than 1. For example, $\frac{5}{8}$ is greater than $\frac{1}{2}$ because $\frac{4}{8}$ is equivalent to $\frac{1}{2}$ and $\frac{5}{8}$ has an additional fourth. $\frac{5}{8}$ is less than 1 because $\frac{8}{8}$ is equivalent to 1 and $\frac{5}{8}$ needs three more $\frac{1}{8}$'s to make a whole. Alternatively, students might draw a number line and show that $\frac{5}{8}$ lies to the right of  $\frac{1}{2}$ (which is equal to $\frac{4}{8}$) and to the left of 1 (which is equal to $\frac{8}{8}$):

  

  • Fractions greater than 1. For example, $\frac{6}{4}$ is greater than 1 because $\frac{4}{4}$ is a whole and $\frac{6}{4}$ has two additional fourths in addition to the whole.

  b. There are many important lessons to be learned from comparing fractions to benchmark fractions, including:

  • The denominator tells me how many pieces to cut my whole into. When the whole is cut into more pieces, the pieces are smaller (this is why $\frac{1}{3}$ is less than $\frac{1}{2}$).
  • The numerator tells me how many equal sized pieces I have. So $\frac{6}{10}$ is more than $\frac{5}{10}$ because I have one extra piece.
  • Fractions are built from the unit fractions so it is important to understand and be able to represent the unit fractions.
  • If using the fraction cards with pictures, equal sized wholes are important when comparing fractions.
  • In a picture of equivalent fractions, the whole is broken into different sized pieces, but the same total amount is shaded.
  • The relationship between the numerator and denominator can help me think about the value of the fraction.
  • Fractions equivalent to $\frac{1}{2}$ have a numerator that is half of the denominator.
  • Fractions equivalent to 1 whole have the same numerator and denominator.
  • When the numerator is a bigger number than the denominator, the fraction is greater than one whole.
  • When doing mathematics, patterns emerge. These patterns support students in making conjectures, supporting their reasoning, and proving mathematical claims.
• Additional Thoughts

Send Feedback