-
- 09/08/13 | Adjusted: 08/01/18 | 1 file
- Grades 3
- 09/08/13 | Adjusted: 08/01/18 | 1 file
Find 1
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: 3.NF.A.2a and MP.1
- Helps students understand fractions in relation to whole numbers 3.NF.A.2a
- Includes an example of a fraction greater than one, allowing students to see that fractions are not limited to values between $0$ and $1$
- Requires students to make sense of the problem and persevere in solving it (MP.1)
In the classroom:
- Engages students quickly without needing much scaffolding by the teacher
- Encourages students to share their developing thinking
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Includes a mathematical routine that reflects best practices to supporting ELLs in accessing mathematical concepts.
- Provides opportunities to support students in connecting mathematical language with mathematical representations.
- Prompts teachers to write essential ideas/concepts/language on the board as a reference for students.
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the major work of third grade Coherence Integrates fractions with whole numbers, and lays groundwork for grade 4 fraction expectations Rigor Conceptual Understanding: primary in this task
Procedural Skill and Fluency: not targeted in this task
Application: not targeted in this task
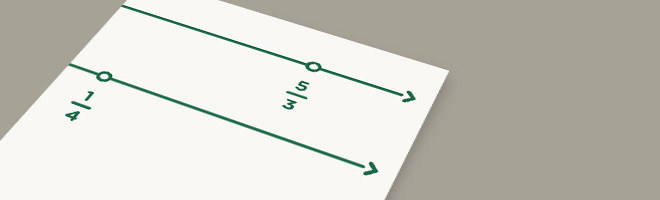
a. Place a point at 1 on the number line diagram below.
b. Place a point at 1 on the number line diagram below.
Commentary:
The purpose of this task is to assess whether students understand fractions as being built from unit fractions and whether they can accurately locate fractions on the number line. Tihs task can also be used in an instructional setting where students work in pairs or small groups to try to figure out how to use the given information to locate other numbers on the number line. If teachers give this task to students without scaffolding, it allows them an opportunity to engage in MP.1, make sense of problems and persevere in solving them. This tasks includes the seeds of several important ideas.
Typically, students start with 0 and 1 on the number line and find unit (and other) fractions. In part (a) students must work in the other direction: they use a unit fraction to find 1 on the number line. This task reinforces the idea that a point on the number line represents a number. This kind of work also lays the groundwork for students to represent addition and subtraction on the number line in grade 4.
Part(b) reinforces the meaning of the numerator and the denominator. When students begin with the interval from 0 to 1, they typically start by partitioning that interval into unit fractions defined by the denominator of the fraction they are given. Here they must start with the numerator because they are partitioning the interval between 0 and $\frac{5}{3}$. This part also helps reinforce the notion that when a fraction has a numerator that is larger than the demoninator, it has a value greater than 1 on the number line.
The following lists related tasks in order of sophistication:
- Locating Fractions Less than One on the Number Line
- Locating Fractions Greater than On on the Number Line
- Closest to $\frac{1}{2}$
- Find 1
- Find $\frac{2}{3}$
- Which is Closer to 1
Solution (using equal intervals):
While it is not necessary to name all of the intervals on the number line, we expect many students will do so.
- There are $4$ fourths in $1$, so if we take the length from $0$ to $\frac{1}{4}$ four times, we will find $1$.
- $\frac{5}{3}$ is $5$ equal pieces where $3$ pieces make $1$. So if we partition the interval between $0$ and $\frac{5}{3}$ into $5$ pieces, each will be a third
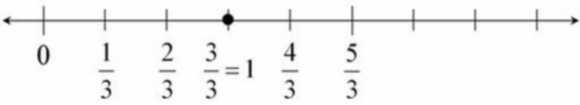
and $3$ thirds is $1$.
3.NF.A.2 calls for students to understand fractions as a number on the number line and to represent fractions on a number line diagram. This is part of the standards' progression toward the rational number system. (6–8, NS).
For more information on the key concepts needed for students to develop conceptual understanding of fractions in grade 3, read pages 2–4 of the progression document, 3–5 Number and Operations – Fractions.
