• Making the Shifts
• Task
• Helen raised \$$72$ this year.

  Commentary:

  The purpose of this task is for students to solve three comparisons problems that are related by their context but are structurally different. Multiplicative comparison is purposefully excluded from third grade (see 3.OA.A.3 and 3.MD.A.2), making this task appropriate for fourth but not third grade.

  In these multiplicative comparison problems, one factor and the product are amounts of money and the other factor represents the number of times bigger one amount is than the other. Sometimes this second factor is called a "scale factor." In part (a), the larger amount (which is the product) is unknown, while in part (b) the scale factor is unknown and in part (c) the smaller amount of money is unknown. Students will study multiplicative comparison problems involving scale factors that are fractions in fifth grade; see 5.NF.B.5. Note that in fourth grade, scale factors must always be bigger than 1, so students often think that "multiplying makes bigger"; however in fifth grade they will see that when the scale factor is less than 1, the product wil actually be smaller than the initial quantity.

  Note that the numbers in parts (b) and (c) are related by the fact family $3×15=45$. This allows for a classroom discussion about the different interpretations of the factors in a mutiplicative comparison context.

  Solution One: Tape Diagram

        a. She raised six times as much money (as shown in the diagram) so she raised $6×12=72$.

  

  Helen raised \$$72$ this year.

       b. $?×15=45$ is equivalent to $45÷15=?$

  

  Nita raised $3$ times as much as Sandra.

       c. $3×?=45$ is equivalent to $45÷3=?$

  

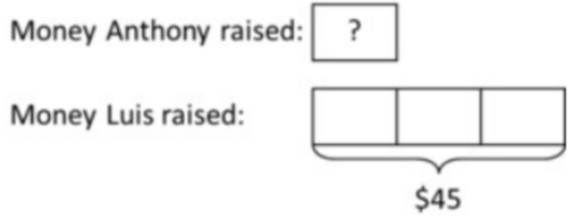
  Anthony raised \$$15$.

  Solution 2: Writing multiplication equations for division problems

       a. Helen raised $6×\$12$ this year, so she raised \$$72$ this year. 

       b. This is a "Number of Groups Unknown" problem. We can represent the question as  $?×15=45$ or $45÷15=?$  So Nita raised $3$ times as much money as Sandra.

       c. This is a "Group Size Unknown" problem. We can represent the question as $3×?=45$ or $45÷3=?$. So Anthony raised \$$15$. 

• Additional Thoughts

Send Feedback