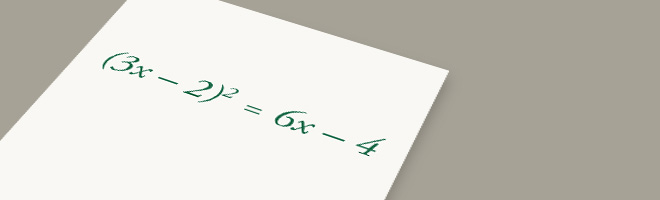
-
- 10/02/13 | Adjusted: 08/01/18 | 1 file
- Grades High School
- 10/02/13 | Adjusted: 08/01/18 | 1 file
Looking For and Making Use of Structure - Quadratic Equations 1
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards:A-REI.B.4 and MP.7
- Rewards the practice of looking for and making use of structure (MP.7).
- Solvable by casting the equation into standard form, although considerable procedural fluency is required for this method. In that case, the task rewards procedural skill as well as perseverance (MP.1).
In the classroom:
- Allows individuals, groups, or the class as a whole to suggest ideas for how to proceed.
- Allows the class to compare multiple methods of solving.
- Does not require extensive setup on the part of the teacher.
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Elicits evidence of student thinking both verbally and in written form.
- Includes a mathematical routine that reflects best practices to supporting ELLs in accessing mathematical concepts.
- Provides opportunities to support students in connecting mathematical language with mathematical representations.
Solve the equation:
$(3x − 2)^2 = 6x − 4$
The practice of looking for and making use of structure (MP.7) often amounts to deferring evaluation. In this case, instead of immediately expanding $(3x − 2)^2$, the student might pause, hold both hands in his or her lap, and examine the structure of the equation. Does any idea come to mind when we see $3x − 2$ and $6x − 4$ next to one another? Solution 1 below develops this line of thought.
Alternatively, Solution 2 shows the route a student might take if he or she is procedurally fluent and has a habit of perseverance (MP.1). There is nothing wrong with this "straight ahead" approach; in fact, it has the virtue of being general. One will note, however, how much longer and more technically difficult that approach is, compared to the approach that exploits the structure of the equation.
Solution 1
$6x − 4$ is twice $3x − 2$, so the equation is
$(3x − 2)^2 = 2(3x − 2)$.
If we put $Q = 3x − 2$, then this is $Q^2 = 2Q$ which can be put into standard form as $Q^2 − 2Q = 0$ and factored as $Q(Q − 2) = 0$. This implies $Q = 0$ or $Q = 2$, i.e., $3x − 2 = 0$ or $3x − 2 = 2$. Hence, $x = \frac{2}{3}$ or $x = \frac{4}{3}$. Both values satisfy the equation.
Solution 2
Expanding, we obtain
$9x^2 − 12x + 4 = 6x − 4$
$9x^2 − 18x + 8 = 0$.
The quadratic formula now gives $x=\frac{(18±\sqrt{324-288})}{18}=\frac{(18±6)}{18}=1±\frac{2}{3}=\frac{2}{3}$ or $\frac{4}{3}$.
Alternatively, one may factor as $(3x-4)(3x-2)=0$.
Quadratic equations come in a variety of forms, such as
$$\begin{align} \\ t^2 &= 49 \\ 3a^2 &= 4 \\ 7 &= x^2 \\ r^2 &= 0 \\ \frac{1}{2}y^2 &= \frac{1}{5} \\ y^2-8y+15 &= 0 \\ 2x^2-16x+30&=0 \\ 2p&=p^2+1 \\ t^2 &= 4t \\ 7x^2+5x-3&=0 \\ \frac{3}{4}c(c-1)&=c \\ (3x-2)^2 &= 6x-4\, \end{align}$$
If a textbook fails to cover a variety of forms – presenting instead problem after problem in standard forms such as $ax^2+bx+c=0$ – then students will not see the true variety of quadratic equations. They may learn stock routines instead of general methods that work for all problems. They may develop "buggy" techniques. And they may not develop the habit of looking for and making use of structure.
For more about the ways in which students should be reasoning with equations, read pages 13 and 14 of the progressions document, High School, Algebra.
