
-
- 10/31/13 | Adjusted: 08/01/18 | 1 file
- Grades 3
- 10/31/13 | Adjusted: 08/01/18 | 1 file
Fraction Comparisons with Pictures, Assessment Variation
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: 3.NF.A.3d and MP.3
- Presents two fractions with the same numerator so that students can compare the size of an area that is 2 one-third sections with an area that is 2 one-fifth sections
- Requires student to recognize that two fractions must refer to the same whole in order to be compared (3.NF.A.3d)
- Builds on student understanding of non-unit fractions as multiple parts of unit fractions (3.NF.A.1)
- Uses rectangular fraction models, which can lead to understanding of fractions on the number line, showing coherence within the 3.NF standards
In the classroom:
- Uses concrete representation to make the mathematics explicit
- Can lead to related discussions with the other fraction comparison tasks
- Presents a task in an assessment-ready form, that is also easily implemented in the classroom
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Elicits evidence of thinking both verbally and in written form.
- Includes a mathematical routine that reflects best practices to supporting ELLs in accessing mathematical concepts.
- Provides opportunities to support students in connecting mathematical language with mathematical representations.
-
Making the Shifts
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the major work of third grade Coherence Lays groundwork for grade 4 fraction equivalence and ordering expectations (4.NF.A) Rigor Conceptual Understanding: primary in this task
Procedural Skill and Fluency: secondary in this task
Application: not targeted in this task
-
Task
- Who correctly compares the numbers $\frac{2}{3}$ and $\frac{2}{5}$?
- Ben said that $\frac{2}{3}$ is greater than $\frac{2}{5}$.
- Lee said that $\frac{2}{3}$ is equal to $\frac{2}{5}$.
- Mia said that $\frac{2}{3}$ is less than $\frac{2}{5}$.
- Compare $\frac{2}{3}$ and $\frac{2}{5}$ using symbols:
$\frac{2}{3}$$\frac{2}{5}$ - Choose the two pictures that best compare $\frac{2}{3}$ and $\frac{2}{5}$.
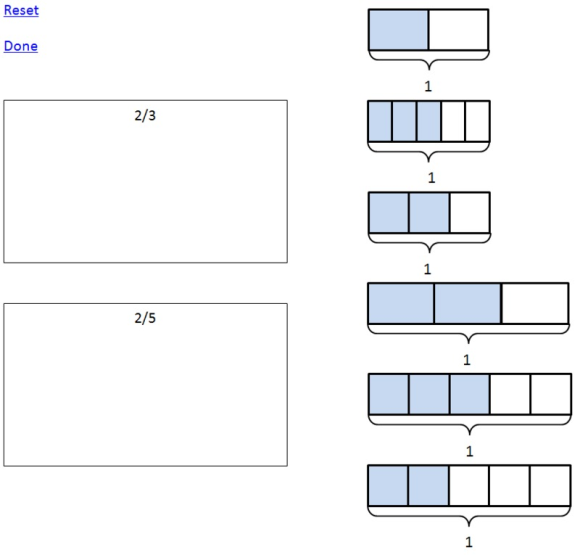
-
Illustrative Mathematics Commentary and Solution
Commentary:
This task is part of a joint project between Student Achievement Partners and Illustrative Mathematics to develop prototype machine-scorable assessment items that test a range of mathematical knowledge and skills described in the CCSSM and begin to signal the focus and coherence of the standards.
Task Purpose:
This task is part of a set of three assessment tasks for 3.NF.A.3d. This part of the standard is about comparing two fractions with the same numerator or the same denominator by reasoning about their size, and understanding that such comparisons are valid only when the fractions refer to the same whole.
3.NF Fraction Comparisons with Pictures asks students to select pictures that accurately represent the relative magnitude of two fractions. This task also requires that students recognize that in order to compare two fractions, they must refer to the same whole.
Mathematical Content:
"3.NF Fraction Comparisons with Pictures" requires students to compare two fractions with the same numerators and then select pictures from a set of choices that can be used to accurately represent the comparison. For the first two tasks in this set, students can choose any method or representation they like to compare the fractions. This task is more complex because students must evaluate pictures they did not draw themselves and must understand that the wholes (rather than the pieces) must be the same size.
Mathematical Practices:
This task partially assesses students' ability to construct viable arguments and critique the reasoning of others (MP.3). Students have to evaluate three different claims and choose the correct one; they also must identify pictures that could be used to support an argument about comparing two fractions.
Solution:
- Ben is correct that $\frac{2}{3}$ is greater than $\frac{2}{5}$.
- $\frac{2}{3}>\frac{2}{5}$
- See video for correct solution.
As part of an assessment, this would be a two-point task:
One point is for correctly determinint that $\frac{2}{3}$ is greater and selecting $\frac{2}{3} > \frac{2}{5}$.
One point is for selecting diagrams that show why $\frac{2}{3} > \frac{2}{5}$.
- Ben is correct that $\frac{2}{3}$ is greater than $\frac{2}{5}$.
-
Additional Thoughts
The video below highlights that in order to compare two fractions, they must refer to the same whole. Notice that the student first moves the "smaller" representation of $\frac{2}{3}$ into the $\frac{2}{3}$ box. However, the student then recognizes that the representation of $\frac{2}{5}$ is "larger" (i.e., represents a different whole) and correctly switches out the representation of $\frac{2}{3}$ for the "larger" one.
As noted in the Commentary above, this task is the third in a set of three tasks. Each task is unique, but all assess various aspects of the same standard. This is important to note when thinking about assessing the full breadth of a standard. The other tasks in the set can be found here: Comparing Fractions with the Same Denominator and Comparing Fractions with the Same Numerators.
For more information on fraction comparison, read page 4 of the progression document, 3–5, Number and Operations - Fractions.
For more analysis on this task from an assessment perspective, read the Cognitive Complexity section on the Illustrative Mathematics site.