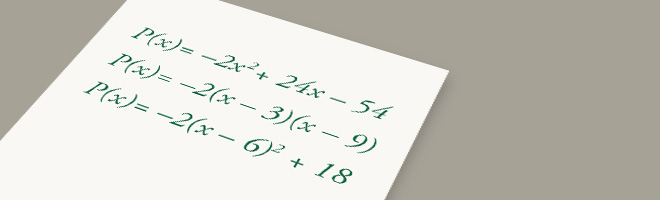
-
- 11/01/13 | Adjusted: 08/01/18 | 1 file
- Grades High School
- 11/01/13 | Adjusted: 08/01/18 | 1 file
Profit of a Company, Assessment Variation
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: A-SSE.A.1, A-SSE.B.3, and MP.7
- Prompts students to analyze three equivalent quadratic expressions
- Allows students to focus on the structure of the expressions without focusing on the procedural skill of factoring or expanding the expressions
- Gives a real-world context for students to interpret the properties of quadratic expressions
- Requires students to look for and make use of structure (MP.7)
In the classroom:
- Offers students and teachers an opportunity to see an assessment-type task with two response types
- Allows teachers to target specific student misunderstanding for reteaching
- With follow-up questions, teacher can prompt students to share their thinking about the concepts in the task
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Elicits evidence of student thinking both verbally and in written form.
- Includes a mathematical routine that reflects best practices to supporting ELLs in accessing mathematical concepts.
- Provides opportunities to support students in connecting mathematical language with mathematical representations.
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the Widely Applicable Prerequisites for College and Careers Coherence Builds on work with algebraic expressions begun in grades 6–8, with added complexity appropriate to high school Rigor Conceptual Understanding: primary in this task
Procedural Skill and Fluency: not targeted in this task
Application: secondary in this task
Commentary:
This task is part of a joint project between Student Achievement Partners and Illustrative Mathematics to develop prototype machine-scorable assessment items that test a range of mathematical knowledge and skills described in the CCSSM and begin to signal the focus and coherence of the standards.
Task Purpose:
The primary purpose of this task is to assess students' knowledge of certain aspects of the mathematics described in the High School domain A-SSE: Seeing Structure in Expressions.
This tasks emphasizes the choice aspect of the full standard, giving students the option of several forms of a quadratic expression to choose from when answering questions about a real-world scenario governed by that expression. The task avoids having the students do the algebraic manipulations themselves, focusing instead on using the structure of the expressions.
Mathematical Content:
Students will likely have encountered several "complete the square" problems which focus on the algebraic manipulation of quadratic expressions. By stripping this procedural aspect of the content away, students are assessed on a more conceptual understanding of quadratic expressions.
Mathematical Practices:
The task, and the standard A-SSE.B.3 in general, ties closely to MP.7, Look for and make use of structure.
At the high school level, structure of the type mentioned in MP.7 manifests itself in the form of algebraic expressions, and the current task concerns itself quite explicitly with exploiting the structure to solve problems. For example, students need to recognize that the structure of the factored form (along with the zero-product property for real numbers) allows them to much more easily find a price that leads to a profit of zero than would, say, the standard form of the quadratic.
Solution:
For each of the three questions, choosing the correct form of the expression allows the answering of the question without doing any computations. Specifically:
- $P(x)=-2(x-3)(x-9)$ shows the values of $x$ that make the profit zero without any computation because a quadratic function in factored form $P(x)=a(x-r_1)(x-r_2)$ has roots $r_1$ and $r_2$ and the profit is zero when $P(x)=0$.
- The profit is zero when $-2(x-3)(x-9)=0$ which occurs when $x=3$ or $x=9$. The company breaks even if the price charged for the product is $\$3$ or $\$9$.
- $P(x)=-2x^2+24x-54$ shows the profit when the price is zero without any computation because the value of a quadratic function in standard form $P(x)=ax^2+bx+c$ when $x=0$ is $c$.
- In this case $c=-54$, so the profit is $-54$ (in thousands of dollars) when the price is zero. If the company gives the product away for free, it loses $\$54,000$.
- $P(x)=-2(x-6)^2+18$ gives us the price which maximizes profit without any computation because the maximum value of a quadratic function in vertex form $P(x)=a(x-h)^2+k$ is $k$ and occurs at $x=h$.
- From $P(x)=-2(x-6)^2+18$, we see that the maximum profit is 18 thousand dollars, and it occurs when $x=6$. The company should charge a price of $6 for this product in order to maximize its profit.
As part of an assessment, this would be a 3-point task.
The Standards avoid the term "simplify" as there isn't always an obvious simplest form. The emphasis instead is on, "purposeful transformation of expressions into equivalent forms that are suitable for the purpose at hand." This task shows three equivalent expressions and requires that students understand the structure and purpose of each one. This is a critical aspect of Seeing Structure in Expressions. For more information on the expectations of this domain, read pages 4–6 of the progression document, High School, Algebra.
For further analysis on this task from an assessment perspective, read the Cognitive Complexity section on the Illustrative Mathematics site.
