In my last post we explored the Most Misunderstood Middle School Mathematics Standards in Grade 6. I have loved the conversations I’ve engaged in with math educators about the post and welcome more people to let me know your thoughts! I can be found on Twitter here: @FLMathNinja.

In this post, we are going to take a dive into the most misunderstood middle school standards in Grade 7. Again, this is not about evaluating or judging teachers, but rather looking at the practice of mathematics instruction in Grade 7 holistically and learning more together about the standards. With that said, these are not the only misunderstood standards, but are those that I have seen the most over the years while supporting teachers.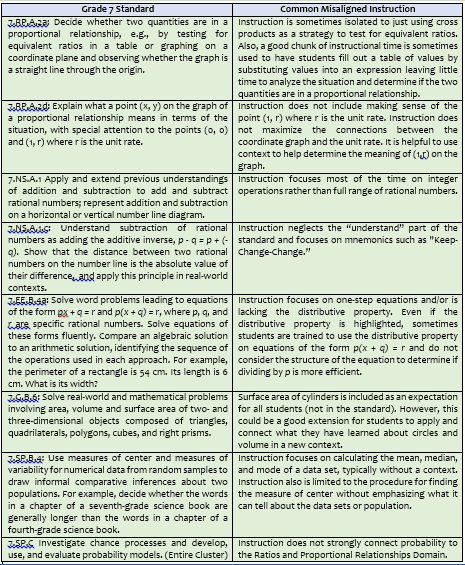

I would like to look more in-depth at two Grade 7 standards, starting with 7.RP.A.2a. This standard gives two examples of methods for determining if a proportional relationship exists by analyzing tables or graphs. Note that using a strategy such as cross products is not part of this standard!  I am going to use an example from a lesson available through the OER EngageNY that could be used to meet the first part of this standard.

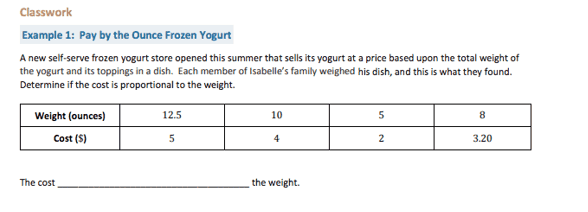In this example, we would want students to reason with sets of ratios to determine if they are equivalent. They could compare different sets of ratios such as 10:4 and 5:2 in the table. Students could also use what they learned from Grade 6 to determine the unit rate from each scenario and use that reasoning to justify if ratios are equivalent or not. In this example, students could reason 10 ounces cost $4, or $0.40 per ounce; 5 ounces costs $2, or $0.40 per ounce. Students could continue using unit rate reasoning for the remaining ratios (12.5 ounces costs $5; 8 ounces cost $3.20) to determine if they also have a unit rate of $0.40 per ounce.

What I also really like about the Frozen Yogurt example is that the table is provided for students to analyze. Sometimes I have seen students struggling to complete the table from a given context or expression. Before long, the bell has rung and students did not spend much time, if any at all, deciding if the two quantities were in a proportional relationship. Keeping a spotlight on the intent of the standard will help you make instructional decisions to maximize the time students spend working on grade-level standards.

The next standard I would like to discuss is 7.EE.B.4a. The standard begins with “Solve word problems leading to equations of the form px + q = r and p(x + q) = r.” For this standard, I have seen a wide range of approaches, from focusing on one-step equations to not including problems of the form p(x + q) = r.  When given an equation such as 5(2+x) many students automatically perform the procedure for distributing without making sense of the structure. This is a chance for teachers to highlight MP 7 (Look for and make use of structure) to set students up for high school work in Algebra . For example, let’s analyze this opening exercise from EngageNY.An equation that can be used to represent this situation is where h = hours per day that soccer was practiced. One way to solve this problem for h is to distribute the 5 and then continue by solving the equation. However, if students are given the opportunity to make sense of the situation and structure of the equation, they could reason the number of practice hours in one day can be found by dividing 20 by 5.  After this step, it would be easy to figure out the value of  h for h + 2= 4 . This type of reasoning is often missing from the Grade 7 classroom. If you want to see an example of a great lesson that highlights this type of thinking, the newly released Illustrative Mathematics curriculum by Open Up Resources has included a lesson on Different Options for Solving One Equation (accessible with a free account). Again, we should have students make sense of the structure of the equation before choosing a method to solve.

As I said in my last post, the suggestions given here are just a start to figuring out this very challenging profession of teaching students mathematics. I hope my experiences in many middle school classrooms will help grow your brain around these standards and now that you know better, you will do better in ensuring each student learns math at a high level. Next month, Most Misunderstood Middle School Mathematics Standards in Grade 8. Stay tuned and #InstructUP!