A Room Full of Wrong Answers
My first Math MilestonesTM task was a disaster. I immediately connected with the idea of students engaging in “the math of the grade level” and having the chance to grapple with rigorous and relevant tasks. Our class was wrapping up our unit on multiplying fractions, so task 5:6, Corner Store, struck me as a perfect opportunity to check in before our summative assessment. My intention was to collect individual responses, select three anchor papers that represented the collective thinking of the class, and have students compare and contrast solution pathways. When I began sorting their responses, I was shocked to see only 15 out of 64 students had the correct answers. A staggering number of students didn’t progress beyond the first part of the question, and I had an alarming number of papers that were almost completely blank. Throughout the unit, my students demonstrated in several ways both conceptual understanding and procedural fluency with fraction multiplication, so what happened?!
Reflecting and Reframing
Starting with my students who had mostly blank papers, I conferenced to understand what had kept them from reaching a solution. 50% misunderstood the context, and 35% had an idea of the answer but struggled to organize and communicate their thinking on paper. Our group of co-designers had just started exploring how highlighting student assets, even in work with incomplete or incorrect solutions, leads to increased agency and a stronger math identity for students. So, I returned to the student work samples and started to highlight, literally, their assets. I highlighted different types of models—number lines, double number lines, fractions bars, pictures that looked like maps of the neighborhood. I highlighted expressions and equations—even ones that weren’t solved. I highlighted math language—numerator, denominator, part, whole, half. As I worked my way through the pile, the job got tougher, as students had less and less visible thinking. Even so, I highlighted sections where students had used both numbers and words. I highlighted multiplication signs denoting they understood the operation of the task. I even highlighted when a student wrote: “I don’t know what to do. Can you help me?” (What an incredible asset to know when to ask for help!) In the end, every paper had an asset highlighted—64 out of 64 students had a starting point. Armed with a stack full of “right” answers, I went back to my students.
Student Sample A
Assets:
- fractions plotted on a number line
- ordered least nearest to 0 and greatest nearest to 1
- represented answer in numbers and words
Student Sample B
Assets:
- use of inequality
- academic vocabulary (“equiv(a)lent”)
- provided justification for answer
Student Sample C
Assets:
- correct initial equation
- shows mastery of adding with common denominators
Assets that Stand the Test of Time
It turns out I was teaching how to DO the math, but not how to SHOW the math—my students needed additional tools to support making their thinking visible. When I teased out the math from the task and provided it as isolated equations, 95% of my students arrived at the correct answer. When I revisited the responses of the students who initially completed the task correctly, I noticed two themes:
- They understood the context and made sense of the problem. (SMP 1)
- They made thinking visible and clear by using precise mathematical language. (SMP 6)
These students had assets that ENDURED beyond a specific context, even as complexity increased, and even when the math was embedded into an unfamiliar context. These were assets I wanted for all my students.
Making Sense of Problems and Persevere in Solving (SMP 1)
Since 50% of my students struggled to make sense of the context, we first worked together to identify barriers. Many students shared that the sheer number of questions within the task was intimidating. With so many numbers, they couldn’t rely on their traditional strategy of “circle the numbers, underline the key words.” We found exceptional success in using Math MilestonesTM tasks from previous grade levels along with the Co-Craft Questions routine:
- Students were presented with a task WITHOUT the question.
- Students recorded their own mathematical questions that could be asked about the task.
- Students shared and compared their questions. Collectively, we kept a class list.
- The actual, intended question was revealed, and students solved the task.
What a joy to see my students able to play in the context of the problem before worrying about getting the “right” answer. Students were immediately engaged because it built on their natural curiosities, and since every question was accepted and validated, everyone had an entry point and felt success. By being given the space to create, compare, and share their questions, students felt competent and in control. Student agency is about voice and choice, so I added the additional option for students to choose one of their classmates’ (or their own) questions to answer as a follow-up to my intended question. This had a very happy, unintended consequence of further solidifying our community of learners—students took such pride in seeing their questions selected and celebrated the hard work of their peers.
A few weeks later, we revisited task 5:6. This time, 44 of 64 students accurately solved all parts of the problem, but more importantly, 56 of 64 students demonstrated—through equations, modeling, or words—that they understood the context of the task. They were making sense of the problem…and 100% of my students persevered to try to solve the task; there were no more blank or nearly blank papers.
Attend to Precision (SMP 6)
Listening to students collaborate during the Co-Craft Questions routine, I was given insight into how they were understanding (or misunderstanding) the context before we solved a problem. Sometimes, like in the case of task 5:1, Juice Box Mixup, it was a matter of clarifying language—“packs” was a barrier for several of my multilingual students.
Student A misinterpreted 240 four-packs as 244 juice boxes and 240 six-packs as 246 juice boxes.
Student B understood the idea of “packs” as groups but reversed the number of packs and the number of boxes of juice in each pack. Highlighting this model as an asset, rather than a wrong answer, led to a rich discussion about the Commutative Property!
Student C demonstrated a clear understanding of packs versus individual juice boxes, which led to not only a correct answer but also a super-efficient strategy.
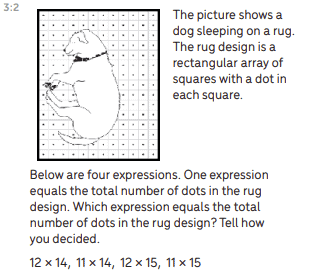
In our early tasks, when students compared their questions, many found the need to add clarity with more precise language in order for their peers to understand their intentions. In task 3:2, Hidden Rug Design, we initially asked, “How big is the rug?” We discovered the ambiguity of the question when we solved the task and came up with two very different, but correct solutions:
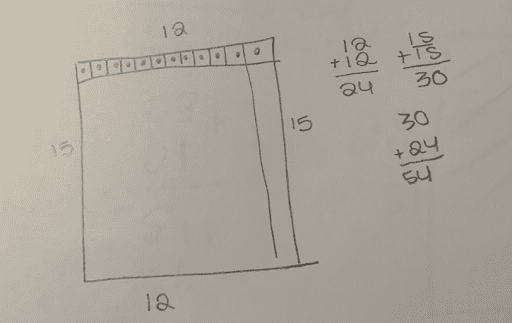
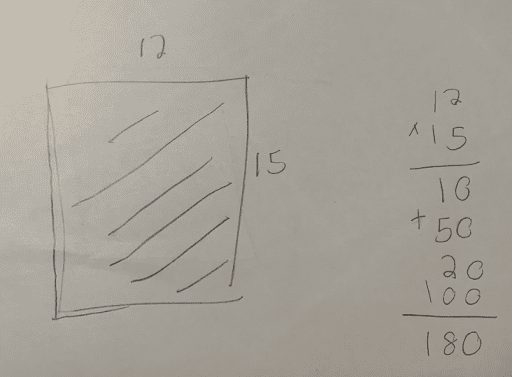
Following the task, I asked, a series of questions:
Teacher: “Which rug is bigger?”
Student 1: “The second one because it equals 180. The first rug was only 54.”
Teacher: “The second rug equaled 180 what? What unit?”
Student 2: “Inches?”
Student 1: “The picture didn’t show inches.”
Teacher: “That’s a great idea; let’s look back at the picture in the task. What unit do you see?”
Student 1: “None. It’s not labeled.”
Teacher: “Is there anything we could measure or count? Even without a label?”
Student 2: “You could count the boxes. There are 180. I counted them.”
Teacher: “So, 180 is the number of boxes in the whole rectangle or the whole rug. What about the first rug; you said that one was 54—does that mean the first rug has 54 boxes?”
Student 2: “But they are the same rug. It’s just one rug. It’s the same picture”
Student 1: “The 54 isn’t the inside; it’s the outside of the rug. It’s the perimeter.”
Teacher: “I see. So, if 54 is outside, the perimeter, what part of the rug is the 180?”
Student 1: “The inside; the area.”
By asking increasingly precise questions, I was able to elicit precise answers. The students understood the difference between perimeter and area, and how to calculate each, but got confused when they each came up with a different solution. The next step was having them revisit their work and add words to help make their thinking more clear. Once we differentiated between perimeter and area, they revised the question to ask, “What is the area of the rug?”
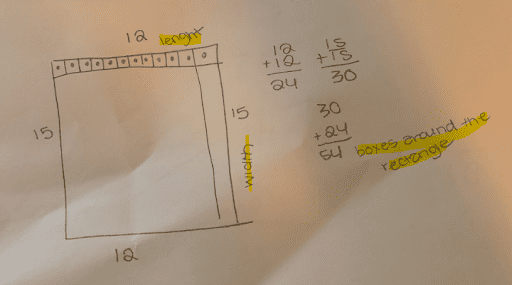
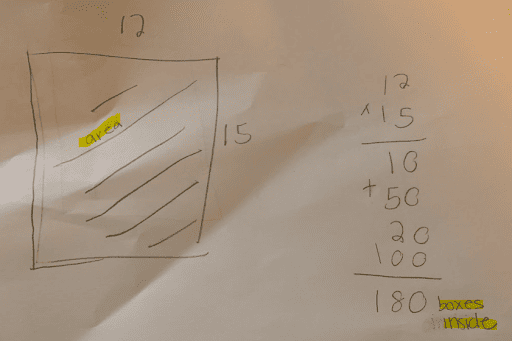
In my classroom of 34 students, it’s impossible for me to dig this deep with everyone, but luckily our students are expert questioners. In terms of teacher moves, I often found my best bet was to get out of their way! With a little modeling and discussion frames, students eagerly took on the role of clarifiers to ensure questions and solutions had precision of language. Their eagle eyes developed by looking at their peers’ work transferred to their own, where I saw a dramatic increase in the number of students who began to use words to label and justify their solutions. Additionally, the opportunities to hear and practice precise, mathematical terms with classmates poured onto their papers. It’s one thing to see a term in a textbook or hanging on a word wall, but quite another to have a low-risk opportunity to try it out.
Lessons Learned
Pacing guides, grades, and state testing are realities that make me nervous about taking the time to try new things like Math MilestonesTM tasks. The seven units of my district-adopted math curriculum are already daunting, so I hardly feel like I have time to add anything else. My year as a co-designer made me realize there’s truth and power in “going slow, to go fast…and making it last!” In a typical year, I set aside 1 day per week designated to reteach and enrichment, plus 2 days at the start and end of each unit to pre-assess and review before our summative assessment. This year, by utilizing the tasks, combined with routines like Co-Craft Questions, I was able to keep the momentum going by building in these opportunities through the tasks.
Reflecting with my students, they didn’t find the tasks to be any more or less engaging than our regular curriculum, but they ALL preferred the community we built around the tasks. They relished the opportunities for collaboration, choice, student voice, and the focus on highlighting and building on assets over getting the right answer. I asked them, “What was your favorite part about math class this year?” The overwhelming answer was “the tasks,” and better yet, “struggling with the hard tasks.” These are the skills and dispositions that will endure. These are the opportunities we owe to our students.


















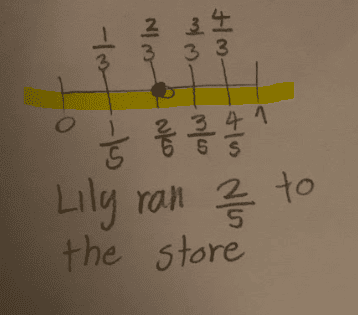
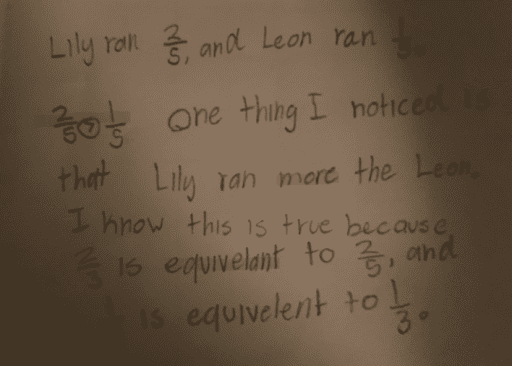
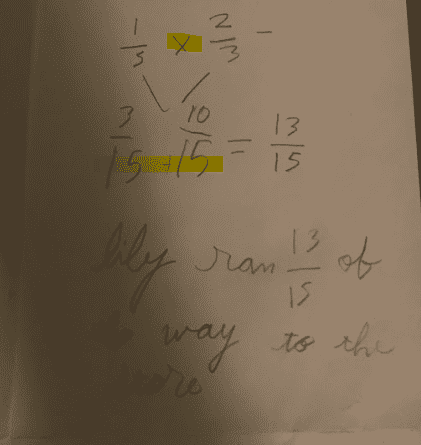

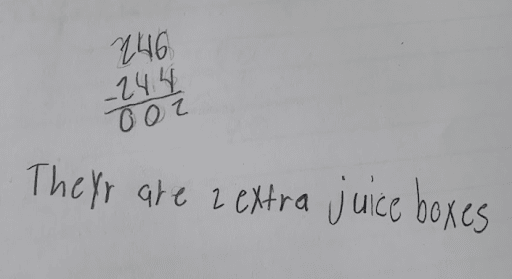
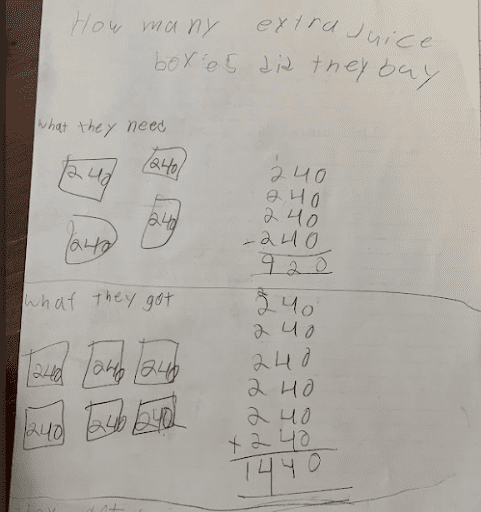


Very interesting when the teacher could not believe now many kids did not solve the problem correctly, so she went to work samples and highlights the assets in each sample, for example, different types of models, expressions, equations, math language etc. The teacher found 64/64 students had a starting point.