When I was asked to expand the series on the Most Misunderstood Standards to grades K, 1, and 2, I jumped at the opportunity. I have four boys of my own at home who frequently say that I never miss an opportunity to talk about math and teaching! I am also an avid reader and user of the previous 3rd-8th grade posts in this series, so I was excited to contribute to it!
In my role as a math coach, and as I travel the country working with educators around aligned math instruction, I have noticed some common themes in K-2 classroom instruction stemming from misunderstanding of math standards. Teaching math in a primary classroom is anything but primary! It is complex work that takes learning and careful attention to instruction, especially as teachers dig into developing students’ conceptual understanding of foundational mathematics in the early grades. I hope this post helps you to reflect and learn to support your young mathematicians!
|
Standard |
Common Misaligned Instruction |
| 2.OA.A.1 Use addition and subtraction within 100 to solve one- and two-step word problems involving situations of adding to, taking from, putting together, taking apart, and comparing, with unknowns in all positions, e.g., by using drawings and equations with a symbol for the unknown to represent the problem. | Instruction is focused on identifying key words to solve the problem.
Instruction emphasizes answer getting techniques rather than encouraging mathematical thinking and meaning making. Instruction does not attend to all 15 problem types for addition and subtraction or neglects the problem types students should master by the end of second grade. We want students to:
*Common Addition and Subtraction Situations can be found here. |
| 2.OA.C.4 Use addition to find the total number of objects arranged in rectangular arrays with up to 5 rows and up to 5 columns; write an equation to express the total as a sum of equal addends. | Instruction goes beyond the grade level standards and introduces multiplication prior to 3rd grade. |
| 2.NBT.A.4 Compare two three-digit numbers based on meanings of the hundreds, tens, and ones digits, using >, =, and < symbols to record the results of comparisons. | Instruction is focused on a procedure without building on place value understanding.
Instruction emphasizes ordering numbers using procedural strategies rather than comparison based on a deepening understanding of three-digit numbers. Instruction treats this learning like a new skill rather than intentionally building on learning from first grade by making connections to comparison of two-digit numbers. We want students to:
|
| 2.NBT.B.7 Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds. | Instruction focuses only on procedural methods for the standard algorithm* without building conceptual understanding.
Instruction is focused on following steps in a procedure and doesn’t build students’ understanding of adding or subtracting like units or composing and decomposing units of tens and hundreds. We want students to:
*The language ‘using the standard algorithm’ is not introduced in the standards until grade 4. |
| 2.MD.B.6 Represent whole numbers as lengths from 0 on a number line diagram with equally spaced points corresponding to the numbers 0, 1, 2, …, and represent whole-number sums and differences within 100 on a number line diagram. | Instruction is focused on a procedure or steps in a process rather than understanding how addition and subtraction of length can be represented on a number line.
Instruction is focused on using a number line as a strategy to add and subtract. We want students to:
|
I would like to take a closer look at two of my favorite standards, both of which call for aligned instruction to build students’ conceptual understanding of foundational math ideas: 2.NBT.B.7 and 2.MD.B.6. Let’s dig in!
2.NBT.B.7
Add and subtract within 1000, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method. Understand that in adding or subtracting three-digit numbers, one adds or subtracts hundreds and hundreds, tens and tens, ones and ones; and sometimes it is necessary to compose or decompose tens or hundreds.
For as long as I can remember as a primary grade teacher and math coach, the standard algorithm for addition and subtraction has been problematic. Students can learn it as a procedure, absent understanding, from well-intentioned teachers or parents. Even I was taught this way as a child! We now know how important it is for students to understand the “why” behind the procedure. It better prepares them for future mathematics and deepens their understanding of place value and the operations of addition and subtraction, which will later be applied in more successful understanding of fraction operations, decimals, and the work of algebra.
When I see a problem like 600 – 432, I know there are many different ways to support students in solving this expression. Students will most likely decompose one of the 6 hundreds into 10 tens and then further decompose a ten into 10 ones. Once 600 is written, drawn, or represented with concrete objects such as base ten blocks or place value disks as 5 hundreds, 9 tens, and 10 ones, students can subtract. It is okay to show this work using a written method that resembles the standard algorithm, if explicit connections are made between the different representations (models or drawings) and the written method. See the example below.
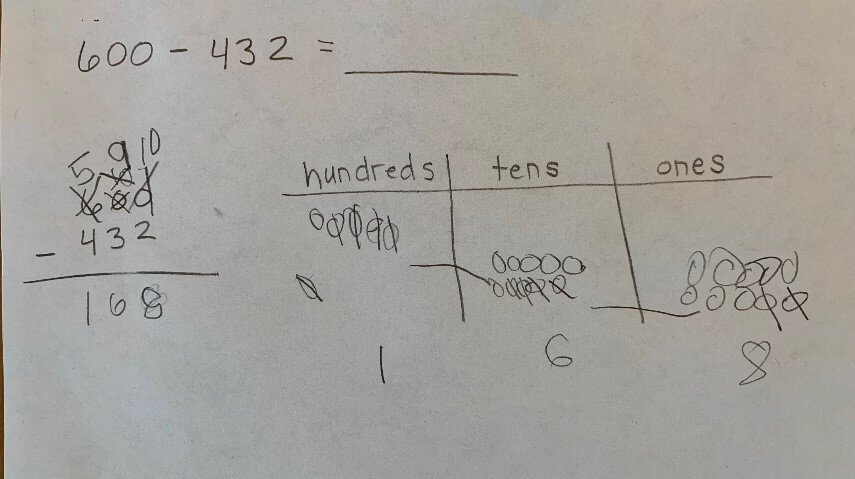
Another way for students to solve 600 – 432 might be by using addition, adding up from 432, therefore emphasizing the connection between addition and subtraction.
The important implication for instruction when working in 2.NBT.B.7 is to not move to procedural teaching before students make sense of the place value system in adding and subtracting within 1000. Give students an opportunity to develop their own solution methods, help them to make connections between representations and methods, and move toward efficiency with the procedure once conceptual understanding has been developed.
2.MD.B.6
Represent whole numbers as lengths from 0 on a number line diagram with equally spaced points corresponding to the numbers 0, 1, 2, …, and represent whole-number sums and differences within 100 on a number line diagram.
I remember at the beginning of my teaching career, 20 years ago (I’m dating myself here!), and for many years after, I taught the number line as a strategy or method for my primary students to add and subtract. There was a cute frog involved and lots of talking about “jumping” on the number line. Students “used” this strategy and arrived at the correct answer most of the time but had no idea what they were doing. They certainly weren’t relating the number line to length units and counting those units. I might still be doing this today had I not engaged in learning from some amazing Core Advocates and teacher leaders!
There are three places in the standards where a number line is specifically called out: here in grade 2, in grade 3 related to fractions as numbers, and again in grade 6 when students delve into rational numbers. It is intentional that the number line is not used prior to grade 2. It is also intentional that it is introduced with counting “length.” It is important to note that the cluster heading for 2.MD.B.6 is to Relate Addition and Subtraction to Length.
Number line diagrams can be tricky for students because they use length units, which are more difficult to see and count than concrete objects or picture representations. Number line diagrams are introduced in grade 2 when students have had experience counting length units on measuring tools, which are essentially special number line diagrams. It is important to support students in “seeing” the length units that are counted in between endpoints as well as the numbers that label the endpoints of lengths from 0.
Let’s look at this task from the Engage NY curriculum:

You will see that students are using a number line to represent length in centimeters. They are adding “more” to a given number, and then writing an equation that matches. This task exemplifies the complexity and intent of 2.MD.B.6 without procedures or an answer getting emphasis.
I hope this has helped you to learn and reflect on powerful, aligned math instruction. I also hope it might provide you with some new ideas for teaching 2nd grade math. I look forward to hearing from you and continuing this conversation! Please leave your comments below or you can find me on Twitter @mrsmillergrade1. Stay tuned for my Grades K and 1 posts as well!



















Our school uses Engage New York Curriculum. What are your thoughts on this curriculum, as far as rigor, alignment, etc? Thanks
Well said! K-2 math is amazingly rich and complex. When it’s taught for finding answers or based on rote learning, the true story is not seen, and the deeper understanding is not built.
I’m retired but trying to help new teachers with ideas
Measuring for the Art Show by Cathy Fosnot is a great resource for introducing the open number line as a model for double-digit addition strategies.
Great stuff. I’d like to see more. I’m going to check out Measuring for the Art Show.
Per pandemic, my 2nd grader is distance learning all this year. I saw every one of the listed issues in his math.
Some problems are solved several different ways, most I had to learn along with him as I never saw those styles even though I have a Math minor.