I was so excited to write this post because I have spent more than half of my 23-year teaching career in 1st grade. I love this grade level, and I especially love the rich mathematical content students engage in during the year of learning!
As I said in my last post, math instruction in the early grades is incredibly complex and standards can be easily misunderstood. That’s why I have studied aligned materials, learned from Core Advocates, and continually deepen my own understanding of math content. Let’s dive into some examples!
| Standard | Common Misaligned Instruction | ||
| 1.OA.A.1 Use addition and subtraction within 20 to solve word problems involving situations of adding to, taking from, putting together, taking apart, and comparing with unknowns in all positions, e.g., by using objects, drawings, and equations with a symbol for the unknown number to represent the problem. | Instruction does not include all the problem types from the Addition and Subtraction chart*.
Instruction on problem types emphasizes some situations more than others and treats addition as more central than subtraction. Instruction includes answer-getting tricks like teaching key words, instead of supporting mathematical thinking and meaning-making. *Common Addition and Subtraction Situations can be found here. |
||
|
1.OA.B.3 Apply properties of operations as strategies to add and subtract.* Examples: If 8 + 3 = 11 is known, then 3 + 8 = 11 is also known. (Commutative property of addition.) To add 2 + 6 + 4, the second two numbers can be added to make a ten, so 2 + 6 + 4 = 2 + 10 = 12. (Associative property of addition.) *Students need not use formal terms for these properties. |
Instruction focuses on procedurally teaching the properties of operations instead of building an understanding of the properties, why they work mathematically, and how they can be used when adding and subtracting.
Instruction emphasizes learning vocabulary, only teaching the terms and their definitions, instead of understanding the mathematical concepts and ideas behind the terminology. Note: Using precise mathematical language is important, but students do not need to memorize or remember the terms. The emphasis is on understanding and using properties of operations. |
||
| 1.OA.D.7 Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false. For example, which of the following equations are true and which are false? 6 = 6, 7 = 8 – 1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2. | Instruction trivializes the meaning of the equal sign by proceduralizing operations instead of building students’ understanding that the equal sign means sameness of the quantities on both sides of the equal sign in an equation (regardless of whether a number or expression is present).
Instruction focuses on always solving each side of the equal sign, instead of sometimes using strategies or mathematical reasoning to determine when an equation is true or false. |
||
| 1.NBT.B.3 Compare two-digit numbers based on meanings of the tens and ones digits, recording the results of comparisons with the symbols >, =, and <. | Instruction does not connect place value understanding that the two digits in two-digit numbers represent quantities of tens and ones to use in comparisons.
Instruction focuses on procedures for comparing numbers rather than understanding quantity of two-digit numbers. |
||
| 1.NBT.C.4 Add within 100, including a two-digit number and a one-digit number, and adding a two-digit number and a multiple of 10, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction, relate the strategy to a written method and explain the reasoning used. Understand that in adding two-digit numbers, one adds tens and tens, ones and ones; and sometimes it is necessary to compose a ten. | Instruction and the problems students are provided are limited to problems with one of the two addends always being a one-digit number or a decade number.
Instruction rushes to the standard algorithm and doesn’t connect concrete and pictorial representations based on place value understanding. |
||
| 1.MD.A.2 Express the length of an object as a whole number of length units, by laying multiple copies of a shorter object (the length unit) end to end; understand that the length measurement of an object is the number of same-size length units that span it with no gaps or overlaps. Limit to contexts where the object being measured is spanned by a whole number of length units with no gaps or overlaps. | Instruction focuses on procedures for measurement instead of building an understanding of iterating length units when measuring (use a single unit repeatedly, end to end, with no gaps, starting at one end point).
Instruction includes measurement using standard units or standard measurement tools such as rulers. |
Let’s take a deeper look at two key standards: 1.OA.D.7 and 1.NBT.C.4. These are both standards that represent Major Work for grade 1 and play an important part in a coherent progression of math instruction in elementary school. I have engaged in a lot of learning around these standards as a teacher!
1.OA.D.7
Understand the meaning of the equal sign, and determine if equations involving addition and subtraction are true or false. For example, which of the following equations are true and which are false? 6 = 6, 7 = 8 – 1, 5 + 2 = 2 = 5, 4 + 1 = 5 + 2.
In my classroom, when I posed true/false problems with an expression on both sides of the equal sign, I used to teach students to always solve both sides first. I would follow that with a comparison of the quantities: if the quantities were the same, then it was true and if not the same, it was false. In talking to colleagues and visiting other classrooms, I have found that many teachers use this same method. In learning more about this standard, I realized I had turned this learning into a procedure, and students ended up with no better understanding of the equal sign.
The aspect of Rigor called for in this standard is conceptual understanding. The mathematical learning goal is for students to understand that the quantities on each side of the equal sign should be the same, otherwise the equation does not make sense mathematically. The equal sign is not about answer-getting, but instead it means something much deeper! It shows that quantities are the same or equal.
Not only was I proceduralizing what should have been conceptual learning, I also missed an opportunity to emphasize reasoning and mathematical thinking based on numbers and operations. For example, in the problem 4 + 4 = 3 + 9, students shouldn’t have to add anything. They should be able to reason that 4 + 4 is not more than 9, and 3 + 9 has to be more than 9, so without adding anything (aside from the known fact 4 + 4) this equation has to be false. Whenever we can emphasize mathematical sense-making in our instruction, we should capitalize on the opportunity!!
1.NBT.C.4.
Add within 100, including a two-digit number and a one-digit number, and adding a two-digit number and a multiple of 10, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction, relate the strategy to a written method and explain the reasoning used. Understand that in adding two-digit numbers, one adds tens and tens, ones and ones; and sometimes it is necessary to compose a ten.
I chose this standard because it is one I misunderstood as a first grade teacher until I had an opportunity to deepen my understanding by digging into standards-aligned curriculum. I thought the standard called for all problems that students work with to look something like 23 + 6, 42 + 4, and 38 + 3, or 23 + 60, 42 + 40, and 38 + 30. In all these examples, one of the addends is always either a one-digit number or a multiple of ten. As it turned out, I misunderstood this standard!
While studying standards-aligned curriculum as a teacher, I encountered many problems like 23 + 36, 42 + 54, and 38 + 27. So how can these two-digit addends match this standard and build toward work that will happen in 2nd grade? I also wondered how to avoid procedural instruction and instead attend to place value understanding with the operation of addition. Let’s look at 23 + 36 and use the student work samples below:

As you can see, in one example, the student decomposed 36 into 30 and 6, then added 23 + 6 as a first step, adding ones and ones. Next, the student added 29 + 30, adding tens and tens, to find the whole amount. This method matches the standard.
In another example, the student decomposed both numbers into an expanded form, then added ones and tens separately (20 + 30 and 3 + 6), and then added 50 + 9. The student in this case used a picture representation and related it to written equations. This method also matches the standard.
Another part of this standard involves understanding that “sometimes it is necessary to compose a ten.” How might a first grade student solve this type of problem (such as 38 + 27) while still attending to the standard? Again, let’s look at student work samples below: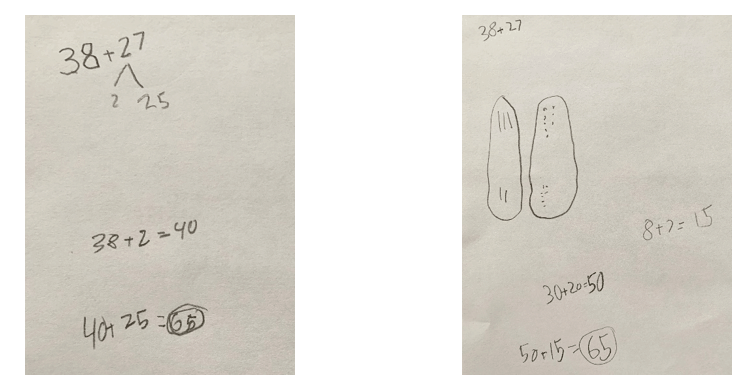
As you can see, one student decomposed 27 into 25 and 2, then added 38 + 2, creating the equivalent problem 40 + 25. This student knew that 2 was needed to make the next decade number 40 and was able to decompose 27 to get the 2. With this method, the student composed a new ten.
Another student added ones to ones, composing a new ten, then added tens to tens using a picture representation based on place value. The student then solved by adding 50 + 15. Both methods are within the scope of the standard.
I love the kind of flexibility allowed for in these problems, setting the stage for different solution methods and different types of student thinking. The solution methods are all grounded in place value and build toward fluently adding within 100 and adding three-digit numbers in 2nd grade, and are foundational for deep understanding of future algorithms.
I hope this post has helped you think differently about the complex math learning that happens in first grade! I would love to read your comments or hear from you on Twitter! (@mrsmillergrade1). I am also moving down the grades with this blog series, so stay tuned for my Kindergarten post coming out next!


















I love this! Thanks for sharing.
I love your entire post, but I really appreciate the way you unpacked the often misunderstood standard 1.NBT.C.4.
Teachers are truly multiplying their efforts to build young mathematicians (Standards of Math Practice) by connecting language routines with multiple representations.
In working with a district using Eureka Math, we found that there is much practice for first grade students using a number line. Is there any support for this method when adding and subtracting or should we hold off until grade 2?
Depending on the problems that are given to students some will naturally lend themselves to using a number line and students can even start creating their own. For instance,
Tim lined up all his train cars to make a train. He saw he had 3 red cars and 2 blue cars. How many train cars did Tim use to make his car? (Trains hook together end to end creating a natural number line.)
A little trickier..Johnny was learning to ride his bike. He used the sidewalk sections (or house lengths) to see how far he had gone on his own. The first time he went only 1 (2,3) section(s). The next time his mom said try to get 1 section more (2 more, etc.) If he went 1 section more how many sections should he count as he tries to go further the next time? (The focus is with distance which naturally lends itself to number line strategy usage.)
Choosing the type of problem strategically will help support the type of strategies you want kids to use. Good luck!
Grades, 1, 2, 3, 4, and 5 examples of core approach. Thx
Love this series of conversations to have with teachers. Is there one for Kinder as well?
Hi Alison: Currently, we do not have one for Kindergarten, but may create a post in the future for this grade level. Stay tuned!
These are super helpful. It would be great to unpack each of the standards as you do for your 2 example standards! Very informative!
I found this article really helpful, thank you. I believe that students need a proper instruction, like tutoring. Math worksheets are great exercises for students to practice what they have learned in class. I found a website that provides free math worksheets, which is called Beestar, their BPE program helps students to build up learning interest, and the most important of doing math exercises is enhancing the grade.
Love these! Is the kindergarten article still in the works? I haven’t been able to find it.
Still in the works. Soon!
I teach math at the High School Level and many of my students struggle with number sense and conceptual understanding of equality. Using the strategies mentioned in this article would greatly curb some of these issues. Thank you for providing this resource, as I will also be utilizing it with my high school students as well.