|
If we had been given these assessments five years ago, we would have still just entered the data in the new datasheet and moved on to the next unit in order to stick with the pacing plan. We would not have felt empowered to spend more time trying to help our students understand the grade-level standards. It would have been about being compliant with the district expectations so “they” could see where our students’ “gaps” are, and not about determining for ourselves what our students know and can do. – Christina & Shelly |
Michelle, Christina, and Shelly are elementary teachers in Newport-Mesa Unified School District and participate in the district math fellows program. Over the past year, they, along with 60 other teachers, have been part of a revised assessment pilot, which you can read about in our previous blog post. In the assessment pilot, teachers use revised assessments developed by the district that focus on the Major Work of the Grade Level with their students, compile student responses into a data table, and join grade-level colleagues in monthly sessions where they analyze their classroom data and collaboratively plan next steps based on their knowledge of their students and the standards. All of this is done with an asset lens; in other words, teachers look for and build upon what students know. We previously discussed using an asset lens in our blog post, What We Pay Attention to Matters.
Michelle’s Experience with Responsive Teaching
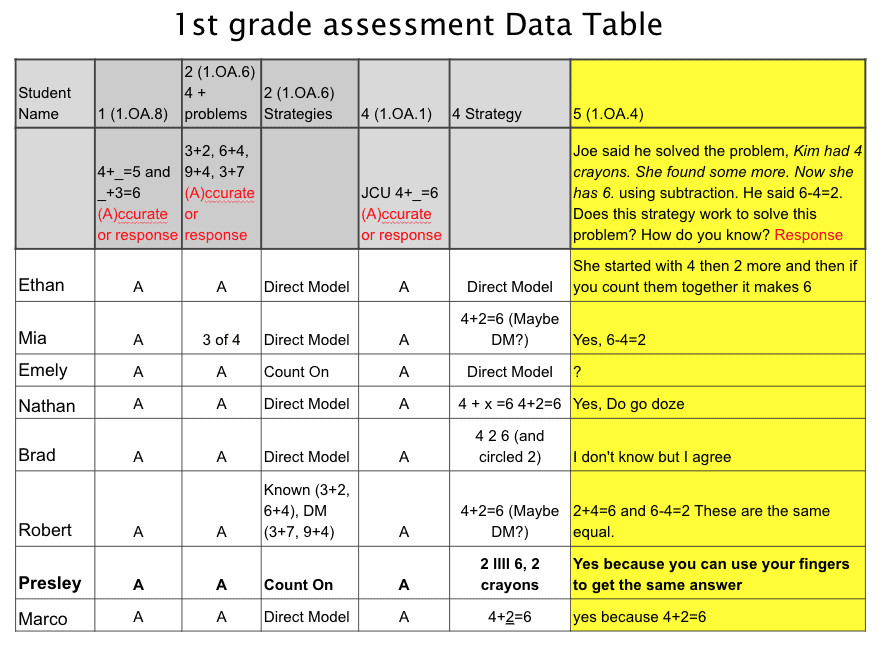
Below, Michelle shares a subset of data from the fall from her first-grade class to show how her sensemaking of the data drives her instructional decisions. Across the top of the data table, you’ll notice the assessment task number along with the standard being measured. For example, “2 (1.OA.6) 4 + problems” means that assessment item 2 measures standard 1.OA.6 and includes four addition problems: 3+2, 6+4, 9+4, and 3+7. “A(ccurate) or response” is the coding teachers enter. If a student is accurate on the problems, “A” is entered into the cell. If a student is inaccurate, their specific response is entered so that teachers can infer student conceptions. The column next to that, “2 (1.OA.6) strategies,” is for teachers to identify strategies students used to solve the problems. In some cases, students used the same strategy for all four problems, and in other cases, see Robert, students used a variety of strategies.
Now let’s drop into Michelle’s thoughts from her data:
Previously, I would have focused only on how many students got the correct answer and then identified who needed more help so that I could remediate their mistakes. Now, I notice how students are thinking and recognize there are multiple strategies being used to solve the addition problems. For example, I see that most students are “direct modeling” (visually representing every addend to find the sum) and a few are “counting on” (abstracting an addend to count on from). As a result, I am able to use this rich data to strategically plan next steps to move students towards counting on.
One way that students often move from direct modeling to counting strategies is through Join Change Unknown (JCU) word problems. In these problems, students have a starting quantity and total quantity and work to find the change. Here’s an example: Brad had 6 toy cars. How many more toy cars does he need to have 10 toy cars?
The data table above shows that all of my students successfully solve JCU problems, a tool I can now use to support the transition to counting. I can also give students problems that start with a high number in order to have students count on from the larger number to get their answer. Understanding what my students’ strategies are can help me build upon that information and give them what they need so they make sense of math.
Notice the data in the highlighted column. Students were asked to evaluate a strategy and determine whether the strategy works to solve the problem and provide reasoning. Instead of looking for mistakes to remediate, I use this assessment data to create opportunities for students to engage in mathematical discourse, listening to how students reason and considering how I might position students as competent mathematicians and contributors to the classroom learning community. For instance, I was drawn to Presley’s response, as it felt accessible to most of my students. They often use fingers or other tools to solve problems and, in this case, Presley has used a representation-based proof. I wondered how Robert and Mia might build on Presley’s thinking to explain what they each meant by their responses. Would this also lead other students to see that connection?
Following my analysis of student data, I would typically engage in a conversation similar to this:
Teacher (Michelle): What do you think Presley means when he says, “you can use your fingers to get the same answer?”
Robert: She means that when you hold up six fingers and put four down, you get the answer two, just like the answer to the word problem. [student holds up his six fingers and puts down four]
Mia: I agree with Robert because that is the same as six minus four equals two.
Robert: Yes it also is the same as two plus four equals six.
As I listened intently to the conversation, I wanted to make space for Brad so he could understand the conversation and be positioned as a competent sense maker. The conversation continued as follows:
Teacher [to Brad]: What does Robert mean “it is the same as four plus two equals six?
Brad: He means this [student holds up two fingers on his right hand and four fingers on his left]. Then he says “six and when I put these four (fingers) down, it makes two.”Teacher [to Emely]: Emely, can you revoice what Brad stated?
Emely: [holds up six fingers (five fingers on the left hand and one finger on the right hand)]Six take away four is two and it is the same as four plus two equals six.” [she puts four fingers down and then puts four fingers up and adds two more fingers to make six]
Unpacking Michelle’s Instructional Moves
Now, let’s step back and unpack the knowledge and beliefs operating behind Michelle’s decisions and instructional moves. Starting with her understanding of student thinking, Michelle has included insight into student thinking within her data table. Rather than marking what students did right or wrong, she’s included details of the strategies students have used to solve each problem; Direct Model (DM), Count On, and Known Fact (KF) are included, showing the level of detail in which she knows her students as learners and her value of their strategies. These terms are part of the shared language she developed through participation in her district’s professional learning and math fellows community. It’s evident that Michelle is not just looking for correct answers. Instead, she is identifying information that will be useful in planning intentional instruction. She sees math as more than answer-getting.
Michelle’s noticing of most students’ direct modeling, identifying the next step as counting on, and suggesting a problem type most useful in supporting her students to count on illuminate her specialized content knowledge (SCK). Her nimbleness in making intentional instructional decisions provided students with rich opportunities to hear and make connections between each other’s brilliant ideas. Instead of grouping or tracking her students by ability, she looked to leverage the assets of students in her classroom to move the thinking of the community forward because she believed they are all competent mathematicians. She noticed Presley’s representation-based proof as she stated, “You can use your fingers to get the same answer,” and encouraged Robert to use his knowledge to demonstrate the relationship between addition and subtraction. Michelle leaned on both of these students, positioning them as competent, within the classroom discussion above. Thanks to Michelle’s belief that students learn from each other, as evidenced through their interactions above, students believe it, too!
Like the teachers whose quote we opened with, Michelle now sees assessment from a much different lens. It’s no longer about giving students a test after teaching a unit, entering data into a district reporting system, assigning students a grade or percentage, and moving on with the next lessons in the instructional materials. Assessment is now seen as the tool it was meant to be: one that provides insight into student thinking at a particular point in time, yielding helpful information to plan next steps to support student learning. Michelle and her colleagues no longer assign a point value or percentage to student assessments. Now they use the information to celebrate and build upon the knowledge and assets their students bring, and leverage those assets to enhance their classroom learning community. Their teaching entails continuous learning and improvement rather than following a script or curriculum.
Reflections on the Impact of Using an Asset Lens
Newport-Mesa district leader John Drake offers his thoughts on using an asset lens:
In my role as the chief academic officer in our district, my hope is that every student and teacher in every classroom has the opportunity to benefit from the thinking and sensemaking that happens when teachers shift to know their students like Michelle demonstrates above. This happens when a teacher engages students in rigorous grade-level learning opportunities, truly believes each student is a capable sense-maker, and positions students as contributors in a community of learners. When these three ingredients are present in a classroom, you’ll see a teacher listening into student conversations and looking at their work products with a lens that focuses on noticing what the students know and understand so that she can respond with a question that nudges the learning forward or leverages a student’s thinking to support the learning of other students in the classroom community.
The same lens that focuses on identifying students’ assets must also be used when using formal assessments. We always say that assessment drives instruction and if this is true, we must use assessment to notice and recognize what students know and understand, and build on these assets instead of identifying what is wrong with students so that we can intervene and fix them. I recognize that this may be a shift in thinking for many and if I’m being honest, it has taken a long time making this shift myself, but it is a critical one. It’s important to acknowledge that this shift requires knowledge, skills, and beliefs. It’s not just about providing a new tool and inserting that new tool into old ways of thinking. We cannot forget that students are people, and assessment must be used by teachers to understand what students know in order to respond in a way that builds on student knowledge. Everyday experiences in our classrooms, including assessment experiences, contribute positively or negatively to a student’s social-emotional well-being. Let us use these experiences in the classroom in a way that positions all students as competent sensemaking contributors to a classroom community of learners.
You can listen to the recording of the webinar, Using Assessments to Foster Agency, Identity, and Learning to learn more about the work these teachers are doing in their district and consider what this might mean for the students, teachers, and administrators in your district, school, or classroom.