.jpg)
-
- 09/08/13 | Adjusted: 08/20/18 | 1 file
- Grades 5
- 09/08/13 | Adjusted: 08/20/18 | 1 file
Box of Clay
- Description
- Files
What we like about this task
Mathematically:
- Addresses standards: 5.MD.C, 5.MD.C.3, and MP.5
- Centers on the fundamental volume concept of the unit cube (5.MD.C.3)
- Connects volume (5.MD.C) to previous multiplicative ideas of times-as-much
In the classroom:
- Gives students the opportunity to develop the method they will use to solve the problem (drawing boxes, using snap cubes, applying the volume formula) (MP.5)
- Encourages students to talk about each other's thinking, in order to improve their mathematical understanding
This task was designed to include specific features that support access for all students and align to best practice for English Language Learner (ELL) instruction. Go here to learn more about the research behind these supports. This lesson aligns to ELL best practice in the following ways:
- Provides opportunities for students to practice and refine their use of mathematical language.
- Allows for whole class, small group, and paired discussion for the purpose of practicing with mathematical concepts and language.
- Elicits evidence of thinking both verbally and in written form.
- Includes a mathematical routine that reflects best practices to supporting ELLs in accessing mathematical concepts.
- Provides students with support in negotiating written word problem
-
Making the Shifts
How does this task exemplify the instructional Shifts required by CCSSM?
Focus Belongs to the major work of fifth grade Coherence Connects volume to multiplication and to addition Rigor Conceptual Understanding: primary in this task
Procedural Skill and Fluency: secondary in this task
Application: primary in this task
-
Task
A box 2 centimeters high, 3 centimeters wide, and 5 centimeters long can hold 40 grams of clay. A second box has twice the height, three times the width, and the same length as the first box. How many grams of clay can it hold?
-
Illustrative Mathematics Commentary and Solution
Commentary:
This task provides an opportunity to compare the relative volumes of boxes in order to calculate the mass of clay required to fill them. These relative volumes can be calculated geometrically, filling the larger box with smaller boxes, or arithmetically using the given dimensions.
The purpose of the task is to help students understand what happens when you scale the dimensions of a right rectangular solid. At some point students need to understand that if you (for example) double the length, width, and height of a rectangular solid, then the volume increases by a factor of $2x2x2=8$. Before they get to the point of generalizing this phenomenon, they should think about the effects of scaling the different dimensions by different factors, as they do in this task.
This is a high-level task for fifth graders, but it fits squarely within the scope of work that students are doing to understand the volume of right rectangular solids with whole-number side-lengths in fifth grade. Depending on how comfortable students are with visualizing rectangular solids, they might benefit from having snap-cubes or some other physical model to help them solve this problem.
This task was adapted from problem #3 on the 2012 American Mathematical Competition (AMC) 12A Test. The responses to the multiple choice answers for the problem had the following distribution:
Choice Answer Percentage of Answers (A) 120 2.08 (B) 160 3.60 (C) 200 5.15 (D) 240 83.82 (E) -- 0.99 Omit 4.33
Of the 72,238 students who participated, 28, 268 or 39% were in 12th grade, 34,124 or 47% were in 11th grade, 4,615 or 6% were in 10th grade, and the remainder were below 10th grade.Solution One: Geometric Visualization
The second box has $3$ times the width and the same length as the first, smaller box. So we can fit three of the smaller boxes inside the second box to make one layer which will be $2$ cm high. The second box is $2$ times as high as the smaller one so we can add one more layer of three smaller boxes to fill the second box.
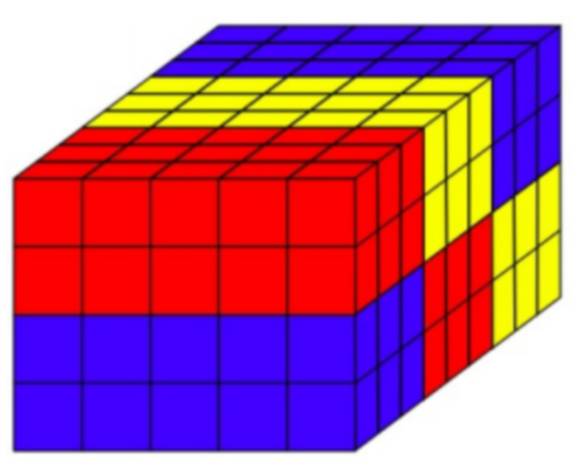
This means that it takes $6$ small boxes to fill the large box so the large box holds six times as much as the small box. Since the small box holds $40$ grams of clay, the large box holds $6×40=240$ grams of clay.
Solution Two: Arithmetic Comparison of Volumes
The first box is $2$ centimeters high, $3$ centimeters wide, and $5$ centimeters long so it has volume
$2$ cm × $3$ cm × $5$ cm = $30$ cubic centimeters
And it holds $40$ grams of clay. The second box is $4$ centimeters high, $9$ centimeters wide, and $5$ centimeters long so its volume is
$4$ cm × $9$ cm × $5$ cm = $180$ cubic centimenters
Since the volume of the second box is $180÷30=6$ times bigger, it can hold $6$ times as much clay. So the second box can hold $6×40=240$ grams of clay.
-
Additional Thoughts
This task could be extended by adding a follow-up with larger numbers. That would enhance the connection to the fluency expectations in the Standards for multi-digit multiplication (5.NBT.B.5)
For more information about the expectation for volume in Grade 5, read pages 26 and 27 of the progression document, K-5 Geometric Measurement.