As the district math coordinator in a school district in Northern California with about 7,000 students, I am often asked: “There is too much to teach…what should I focus on?” Lately, I have been giving a two-part answer. I first point to the Focus document, which gives teachers a framework for how to think about what content in their grade level they should focus on. The second part of the answer is that they should focus on activating a robust student identity. I believe this happens when we make math class about sensemaking instead of answer-getting.
The Math Milestones initiative has given me an opportunity to build a bridge between sensemaking and essential mathematics. This fall, I have used Math Milestones tasks in classrooms to teach two-day lessons that involve a three read protocol and a re-engagement structure.
This is how this two-day lesson played out in one third-grade class. The lesson was based on Math Milestone task 3:1, Volleyball Players:
Day 1
I find a good way to make a classroom a sensemaking space is to give a task to students prior to a unit of study that addresses the central mathematics of the task. By doing this, students are not relying on trying to remember how their teacher “taught” them how to solve the problem. Instead, students find themselves in a place where they need to rely on prior knowledge and the task’s context to make sense of the problem. As students have experiences like this, they come to realize that they can work on something until it makes sense rather than having to wait to be told what to do. This activates their agency and strengthens their mathematical identity.
I gave this Volleyball Players task to third graders about one month into school and before much instruction on multiplication.
To support sensemaking, I utilized the Three Read Protocol during Day 1. There are different ways people do the Three Read Protocol but in the version I use, I start by giving students the “problem stem,” which is the problem with the question removed. Then, during the third read, we ask, “What questions can we ask?” After students share their questions, I reveal to students the question I want them to answer.
A few things struck me as students made sense of this task on Day 1. Most of the students in this third-grade class are multilingual students. By the third read, I was aware that language in the problem stem was a barrier to some students’ ability to make sense.
We stopped for a moment and showed a video of a volleyball game. More importantly, we discussed what a “league” was because this was mathematically important in this problem. Interestingly, a league is a group of groups.
I did not see a lot of evidence of students making sense of this problem as they worked on the question of how many players were in the league nor when I analyzed the work after the lesson. To be clear, this does not mean they were not grappling with it and doing some sensemaking; I just wasn’t seeing the evidence of this thinking. However, the evidence that they provided me did inform my next steps. Here is a breakdown of the work that was analyzed after the lesson:
| Lack of Evidence | Multiplication (5 x 6) w/o explanation | Repeated addition w/o diagram | 5×6 w/ explanation | Repeated Addition w/ diagram |
| 5 | 4 | 2 | 4 | 2 |
In addition, I only saw a couple of diagrams. All this informed the re-engagement lesson I would be conducting on Day 2. I wanted to provide more experiences for students to engage in sensemaking and that would also elicit evidence of how they were thinking about the context and its connection to multiplication.
Day 2
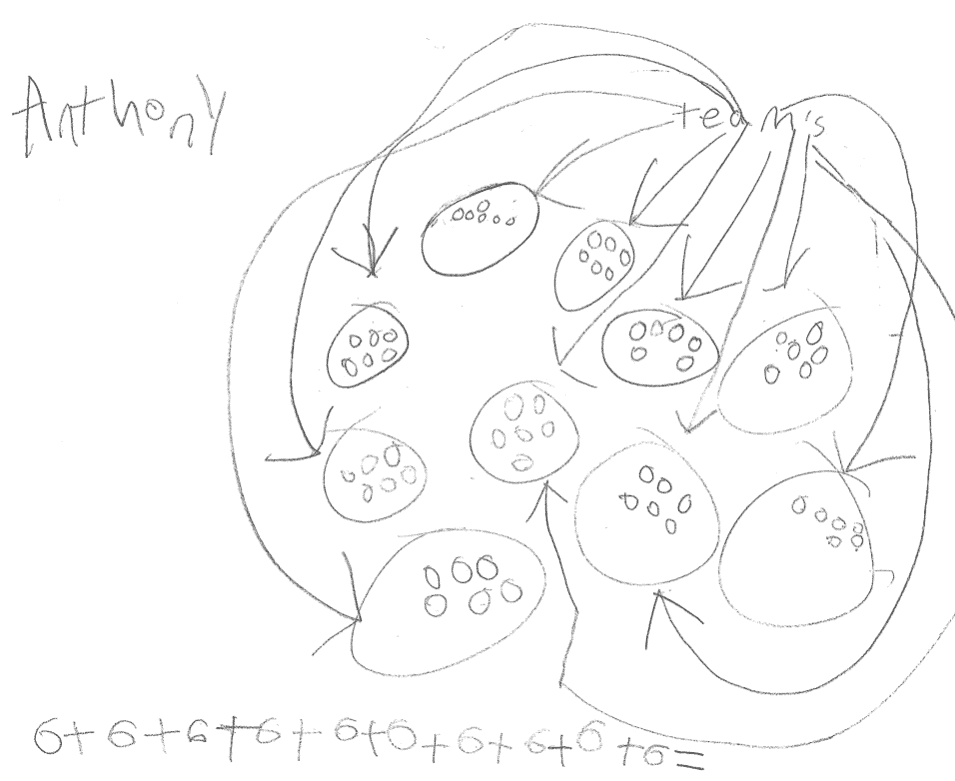
Based on this data, I designed a re-engagement lesson that would support students in making connections between the context, the diagrams, repeated addition, and multiplication. The lesson would center around these two pieces of student work from Day 1. When choosing student work for the re-engagement lesson, I wanted to build a bridge between the sense students were making and the essential mathematics of third grade. Student A provided a diagram and the repeated addition expression, which offers an opportunity for students to see the problem through the lens of second-grade math content. In addition, by privileging work with a diagram, this could possibly activate students’ agency to use diagrams to make sense of a problem. Student B’s work allows for the connection to be made that the third-grade essential mathematics of multiplication is a way to represent equal groups. It also makes another connection to the addition.
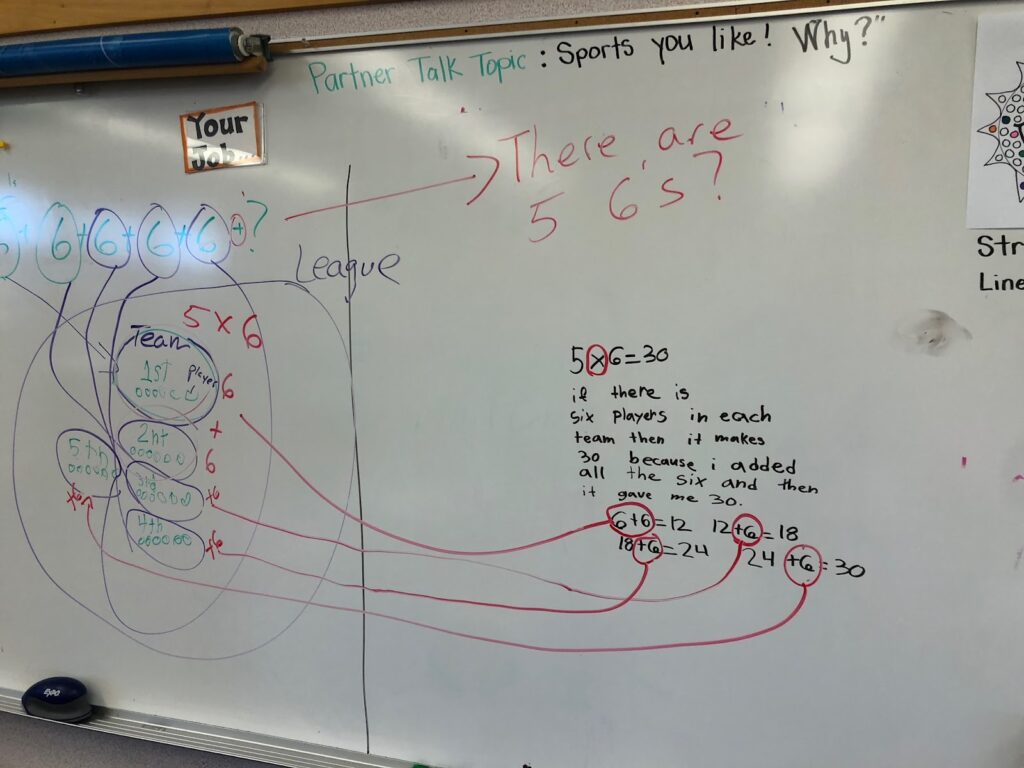
With the work on the right, we established that those were teams, and the whole diagram represented the league. Then I directed their attention to the 6s in the addition equation model on the bottom. I circled the first 6 and asked them, “Where is this 6 in the diagram?” Students struggled to make a connection between the 6s in the equation and the six circles that made up a team in the diagram. To solidify this connection, we repeated it for the rest of the 6s, one by one. Then we found the 6s from the second piece of work. Students at this point were making fragile connections between the abstract models and the diagram.
This is what the board looked like after this conversation:
At this point, the class had done lots of deep thinking about this problem, and I almost left it there, but I was a little unsure of how far they had moved in their understanding of multiplication. So I gave them this prompt: “There are ten teams in the volleyball league. Every team has six players. How many players are in the league?”
I was quite pleased with the growth they showed in just two lessons. About 14 of the students produced a diagram, and 12 of those showed evidence of connecting to the context and diagramming 10 groups of 6. (You can see a couple of examples below.)
After this experience, I was left convinced that students can learn important mathematics when the lesson centers on having them make sense. Not only can they learn essential grade-level mathematics in this way, but they also come to identify themselves as doers of mathematics. This activating of their robust math identity can and will be leveraged in many other contexts.
During these two days, they were asked to make sense of a context, each other’s work, and connections between repeated addition, multiplication, diagrams, and the equation model. As the evidence shows, while the understanding is new and fragile, these students took large strides towards some of the most important work in third grade in just two days. The work below shows a couple of examples of the important mathematical sense students engaged in after only two lessons.

















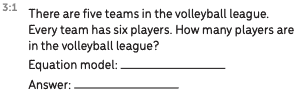
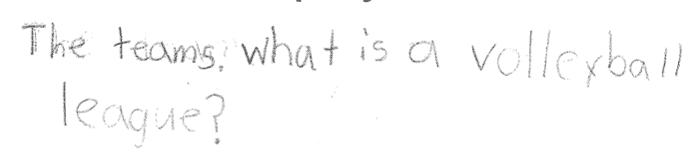

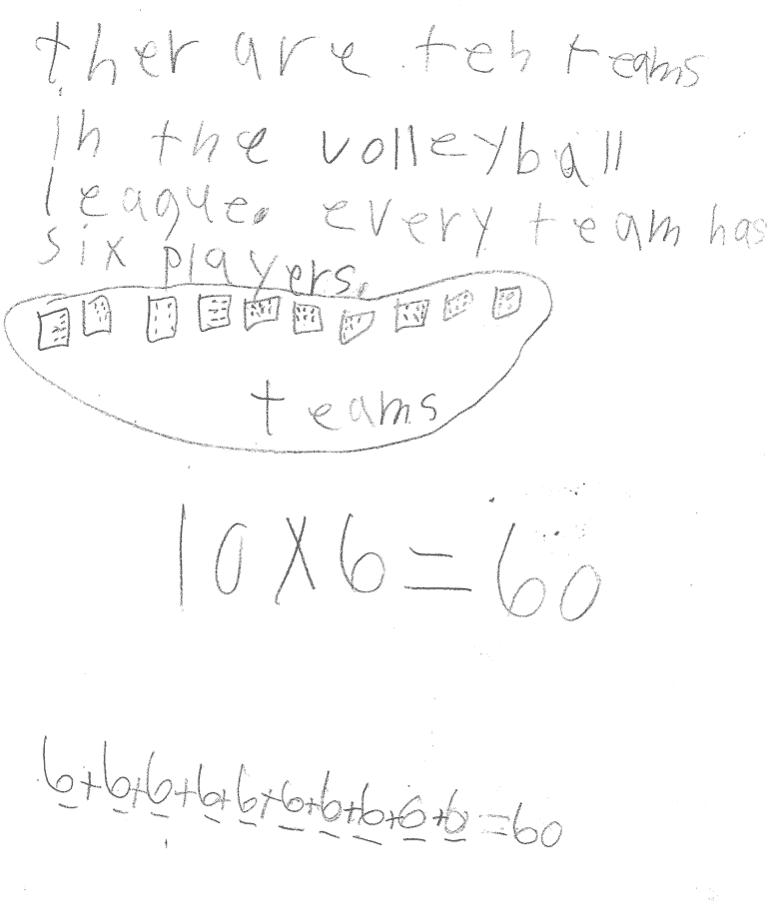

This is a clear example of how we can help students move their math thinking forward by taking time to analyze student work and carefully craft the discussion phase of a problem based lesson.
This clearly illustrates a few things that have been on my mind lately, robust integrated English Language Development embedded into all subject areas and breaking the initial word problem prompt into a problem stem. Taking the time to remove the obstacles of vocabulary was the first valuable step of this problem. Removing the question is such a fantastic way to encourage the students to isolate and diagram the essential information. Once they have their information diagrammed, the question seems more manageable. Great work with your patience and persistency.
Very informative article. Looking forward to trying this out in the fall with my fourth graders. Loved how kids looked at each other’s work samples to make sense of it all leading to rich conversations.