In this six-part blog series, Chrissy Allison and Becca Varon will illustrate how to make some of the trickiest standards in grades 6-8 accessible for all students and provide concrete examples of how math educators can address unfinished learning within the context of grade-level lessons, which in the long term will help prevent an entrenched pattern of over-remediation and below-grade-level teaching. You can read their introductory post here.
In this third post, we will explore ways to “bridge the gap” with the 7th-grade standard 7.EE.A.1.
Let’s take a look at the standard itself. As you read, consider how it compares to the teaching methods and strategies you use:
| Cluster 7.EE.A: Use properties of operations to generate equivalent expressions. 7.EE.A.1: Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients. |
Ah, “properties of operations.” If we think of the standards in terms of anatomy, then the properties of operations are the spine. They stack up vertically through every grade from 1st to high school, providing strong and flexible connections from concept to concept. There are a whopping 23 individual standards that mention the properties of operations by name. If you teach math, you teach something connected to the properties of operations.
However, since most math teachers haven’t worked across elementary, middle, and high school contexts, it’s common to lack full context about where the properties of operations come from and where they’re going. In theory, high schoolers should instantly see that polynomial operations draw on the same strategies they’ve used since elementary school. But instead of building on their prior knowledge of area models and the distributive property, many are taught to “FOIL” without understanding why.
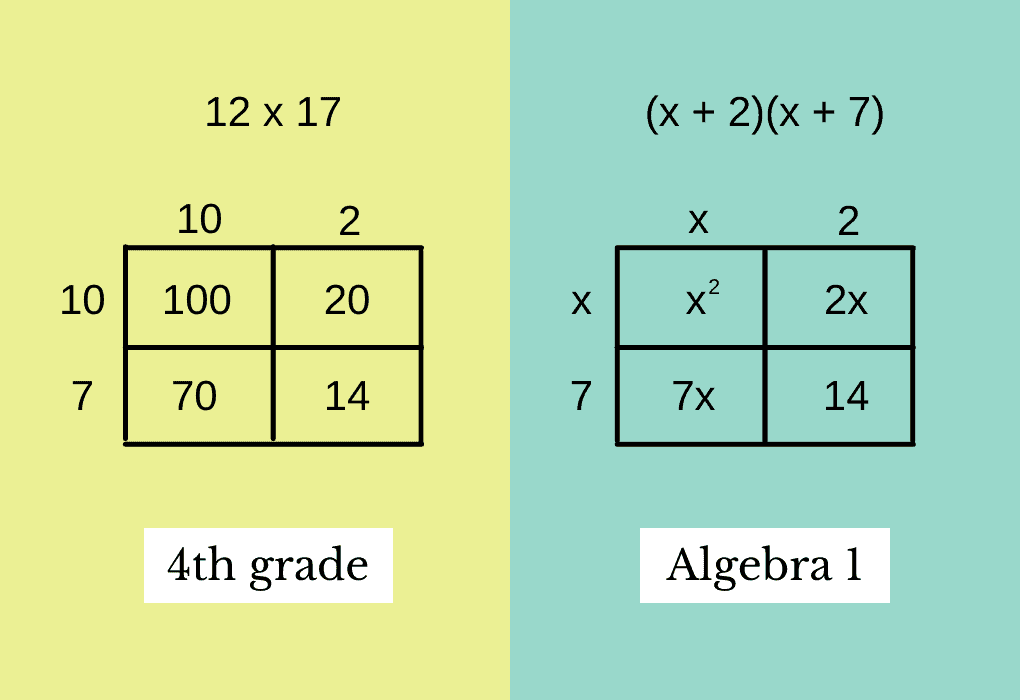
How can we ensure that students maintain focus on these powerful structures (Standard for Mathematical Practice 7) and don’t end up seeing math as a set of fragmented tricks? Building strong connections through the middle school bridge just might be the key. Let’s do a close read of this standard to understand it more deeply:
| Cluster 7.EE.A: Use properties of operations to generate equivalent expressions. 7.EE.A.1: Apply properties of operations as strategies to add, subtract, factor, and expand linear expressions with rational coefficients. |

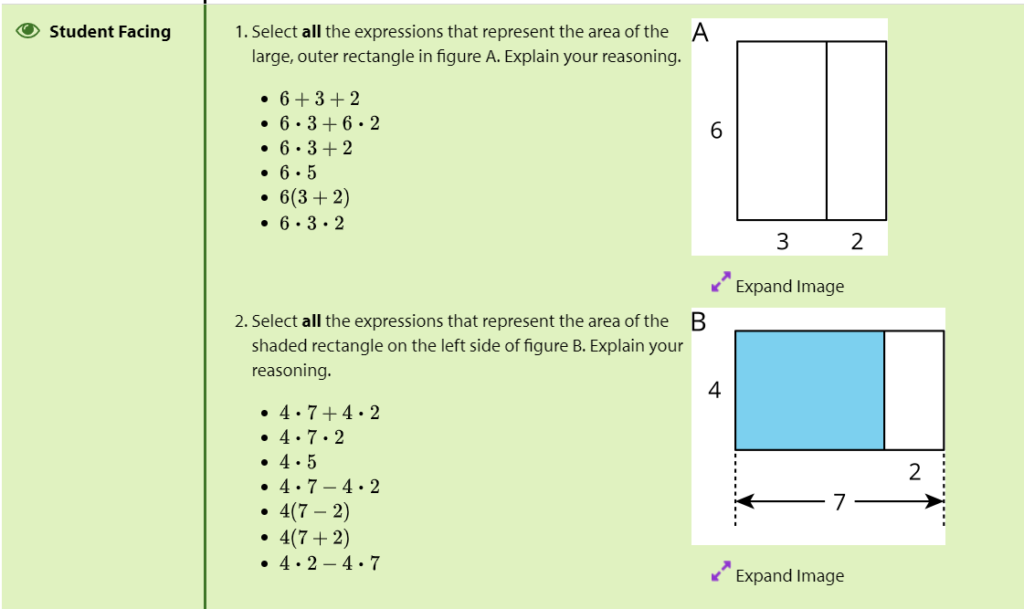
Now, let’s look at an example task from a lesson in the Illustrative Mathematics (IM) curriculum that aims to build from conceptual understanding towards procedural skill. I encourage you to pick up a pencil and do the math to better understand what’s being asked of students:

One reason to be excited to teach this task is that it models to students that answer-getting isn’t actually our primary goal. We need to actually be able to explain our thinking, which will start to shake the dust off of concepts and vocabulary relating to the distributive property.
But what if we’ve diagnosed that students need some help with the foundational concepts of the distributive property? For example, what if students have trouble factoring or expanding expressions without variables? Fortunately, the properties of operations are forgiving. Each “at-bat” in each grade provides a new opportunity to explore them conceptually. While it’s absolutely worth investing a little time at the beginning of a lesson to strengthen that foundation, you may be surprised to find that most students will be ready to engage with grade-level concepts almost immediately with a little ongoing support.
There are a number of ways you might take action to address this unfinished learning during the first few parts of this task:
- Solve a quick, analogous task with whole numbers: IM’s diagnostic for this unit suggests using a task like this one to build a bridge to grade-level content. While this task is from a 6th-grade lesson, it is designed to activate knowledge about the distributive property from 3rd grade. Students who need even more support with this might be encouraged to tile (draw a grid on) the rectangles to more concretely see the connection between multiplication and area.
- Leverage pictorial models: Area models, like the ones used above, can easily transition into tape diagrams and can also be used in concrete forms if necessary. Invite students to continue using these models throughout the lesson.
- Reinforce key concepts about variables and equivalence: In 6th grade, students learned that expressions are equivalent when they “name the same number regardless of which value is substituted into them” (6.EE.A.4). Continually revisit this idea by encouraging students to experiment with different values for the variable, investigating whether they really do reveal equivalence between expressions. This is conceptual understanding that will continue to serve students well long after middle school.
We hope this example was helpful as you work to “bridge the gap” to grade-level math. In the comments, please share how your students responded to the adapted task, additional scaffolding ideas, and any feedback you have.
For more examples, be sure to check out our previous post on 6th-grade standard 6.NS.A.1, as well as other forthcoming posts on 7th- and 8th-grade standards in the Middle School Unfinished Learning series.



















