Welcome back to the Unfinished Learning in Middle School Math series, in which math educators Chrissy Allison and Becca Varon illustrate how to make some of the trickiest standards in grades 6-8 accessible for all students. Over the course of six blog posts, we’ll provide concrete examples of how math educators can address unfinished learning within the context of grade-level lessons, which in the long term will help prevent an entrenched pattern of over-remediation and below-grade-level teaching. You can read our introductory post here. In this fifth post, we will explore ways to “bridge the gap” with the 8th-grade standards 8.EE.C.7 and 8.EE.C.8.
Let’s take a look at the standards:
| 8.EE.C.7 Solve linear equations in one variable. 8.EE.C.8 Analyze and solve pairs of simultaneous linear equations. |
Ah, solving equations—an essential skill students need to be successful in Algebra I and beyond. Whether students are working with inequalities, quadratics, or exponential functions in high school, they’ll leverage skills and understanding they developed in the elementary and middle grades.
8th grade is not students’ first encounter with finding missing values in a number sentence. In fact, with the introduction of college- and career-readiness standards, many students have been solving word problems “with unknowns in all positions” using “a symbol for the unknown number to represent the problem” since 1st grade (1.OA.A.1).
Despite the ongoing focus on algebraic thinking in grades K-5, and a continued emphasis in grades 6-7, it’s not uncommon for 8th-grade students to enter the year with a shaky understanding of how to solve equations. In fact, it’s likely the number one concern we hear from 8th-grade teachers who ask, “How can I teach students to solve multi-step equations and systems of equations when they can’t solve simple one-step equations?”
Before we share ideas to help address students’ unfinished learning with equations, let’s take a moment to study and understand these two 8th-grade standards:

To anchor the discussion about how to address students’ unfinished learning with equations, we encourage you to take a minute or two to solve the problem below, which is aligned to standard 8.EE.C.7. As you do so, think metacognitively about the steps you’re taking, the purpose of each step, and how you decided what to do next.

Solving this problem involves the distributive property, combining like terms, and operations with rational numbers. Not only that, but there are myriad decisions students must make in order to isolate the variable and find a solution—and more than one way to do so.
After solving the equation above, can you see why a teacher might hesitate to put multi-step equations in front of students who have struggled to solve simpler, one-step equations involving positive whole numbers?
In fact, when teachers diagnose unfinished learning in this area, many assume they must start back at square one, helping students solve the most basic equations before working their way up. However, much of the conceptual understanding and procedural skills that are necessary to solve complex equations overlap with those necessary to solve simpler equations.
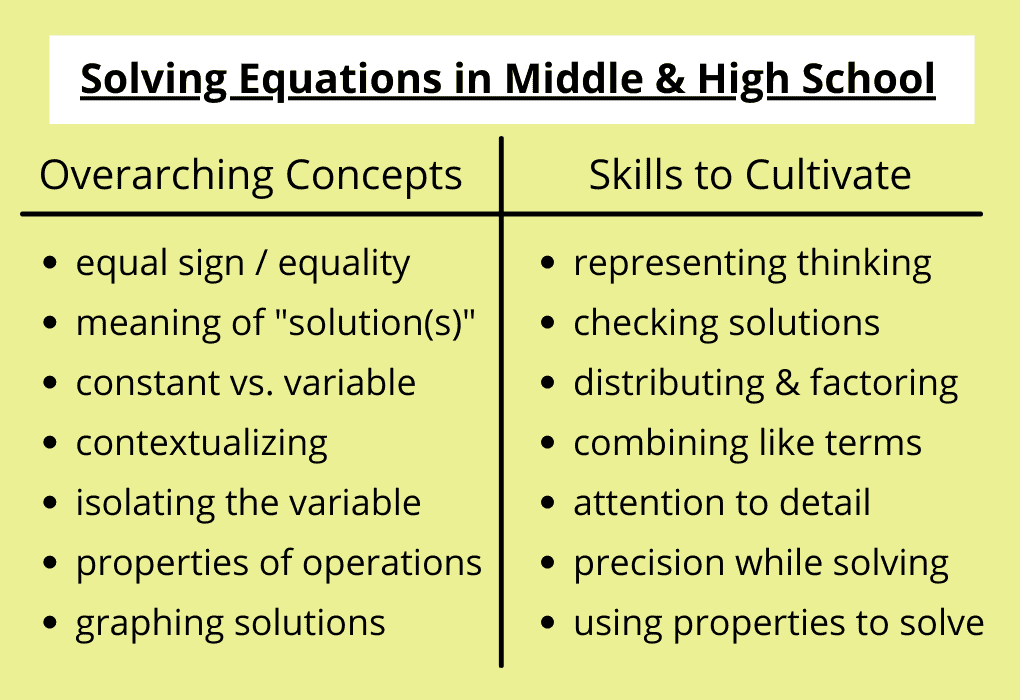
As a result, when teachers identify students needing additional support, they have the opportunity to strengthen prerequisite skills and concepts alongside the 8th-grade content.
Below are some ideas of how to take action to address students’ unfinished learning while moving forward with grade-level content:
- Reinforce important concepts, such as the meaning of “solution.” Rather than solving a series of 6th-grade tasks, reinforce important ideas such as the meaning of solutions and the difference between “constant” and “variable.” This can be done within the context of grade-level aligned problems such as two-step equations, multi-step equations involving the distributive property, and system of equations. The Solving Equations task and The Sign of Solutions task, both from Illustrative Mathematics, provide opportunities to deepen understanding of these concepts.
- Emphasize the properties of operations instead of step-by-step procedures. Teaching students to solve one-step equations by identifying the “inverse operation,” doing the “same thing to both sides,” and “canceling terms” is commonplace in 6th-grade classrooms because they work for the majority of simple equations students are solving. However, they do not set students up for success in future grade levels when students solve increasingly complex equations. By focusing more time and attention on the why behind each step, students use reasoning to make decisions, think flexibility while solving problems, and deepen their understanding of concepts like equivalence and equality. Check out our previous blog post about addressing unfinished learning when teaching the properties of operations here.
- Engage students in tasks with multiple entry points and solution pathways. Assign problems that are set in a real-life or mathematical context. Allow and encourage students to find solutions using strategies other than writing and solving an equation. Then, invite students to share their different approaches with the class. Ask questions to probe students’ thinking and help them make connections between strategies. Want to try it out? Kimi and Jordan and Fixing the Furnace from Illustrative Mathematics are tasks that provide access for students no matter where they are in the learning progression. At times, you may want to modify a task to increase accessibility for students. For example, the Summer Swimming task from Illustrative Mathematics can become more open-ended by reordering pieces of the task. Try assigning Part E first, then having a brief class discussion about ways students approached the problem. This will prepare students for Parts A-D by helping them make sense of the problem context first without the expectation to represent it using an equation.
We hope the ideas shared here will help you create an on-ramp for students with unfinished learning in the expressions and equations domain. We’d love to keep the conversation going in the comments by hearing from you! Please share:
- What approaches have you used to “bridge the gap” to multi-step equations?
- How have you helped students find success with systems of equations?
Finally, don’t forget to check out other posts in the Unfinished Learning in Middle School Math series for additional strategies, examples, and ideas.