In my last post we explored the Most Misunderstood Mathematics Standards in Grade 3. It has been thrilling to see the reactions on both Twitter and Facebook. I would love to continue to engage with math educators and can’t wait to hear your thoughts! Leave me a comment below!
In this post, we will dive right into the most misunderstood math standards in Grade 4. I want to say again this is not an evaluation of teacher instruction in Grade 4; rather, it is a place where we can learn together about the current state of instruction in fourth grade and name concrete ways to get better. Together!
Two of my favorite standards in Grade 4 require us develop conceptual understanding in order to reach procedural skill: 4.NBT.B.5 and 4.NBT.B.6. Let’s dig in!
4.NBT.B.5
Multiply a whole number of up to four digits by a one-digit whole number, and multiply two two-digit numbers, using strategies based on place value and the properties of operations. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
In Grade 4, students are introduced to an area model for multi-digit multiplication, which connects to the 3rd grade understanding that the area of a rectangle is the product of its width and length. For this blog post, we will examine the connections between the area model, partial products, and the distributive property for two-digit by two-digit numbers.
Illustrating partial products with area models (Examples from the Progressions Documents found here.)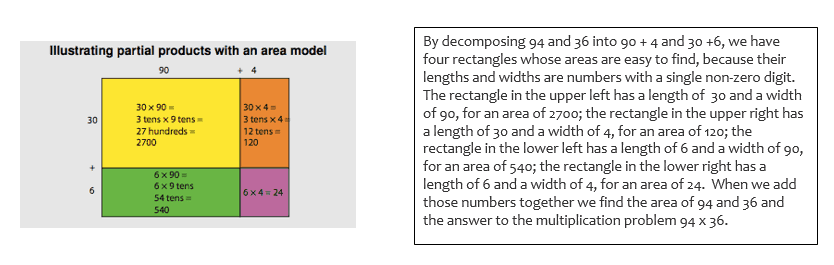
The example on the left is an area model illustrating partial products. Partial products uses place value concepts to solve multi-digit multiplication problems. It’s based on the distributive (grouping) property of multiplication. “The distributive property allows numbers to be decomposed into base-ten units, products of the units to be computed, then combined. By decomposing the factors into base-ten units and applying the distributive property, multiplication computations are reduced to single-digit multiplications and products of numbers with multiples of 10, of 100, and of 1000. Students can connect diagrams of areas or arrays to numerical work to develop understanding of general base-ten multiplication methods.” The area model provides us with a pictorial representation of the concept we want students to understand and makes the important connections to place value explicit for students.
4.NBT.B.6
Find whole-number quotients and remainders with up to four-digit dividends and one-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models.
Similar to multiplication, we will examine division using an area model to illustrate partial quotient.
In partial-quotient division, place value and an understanding of multiplication are used to find partial quotients.
Historically, multi-digit division and multiplication have been solved by memorizing steps, mnemonics, or acronyms without connections to place value, area, and the properties. How many of you have heard Does McDonald’s Serve Cheese Burgers when discussing fourth grade division instruction? Be honest! I certainly will. Before I knew how important understanding the math concepts underpinning multiplication and division were, I thought a catchy phrase was just the thing to help my students remember steps to solving a problem. However, the saying, Does (division) McDonalds (multiplication) Serve (subtraction) Cheese (check) Burgers, (bring down) misses the mark when we think about deeply understanding division concepts.
Let’s make a commitment to one another. We commit to teaching the concepts of multiplication and division. We will not use acronyms or mnemonics to teach important math concepts. We can do it!
Thank you for your commitment to excellent daily math instruction for all students. See you next month when we dive into Grade 5.



















Thank you so much for your posts! I find them quite helpful.
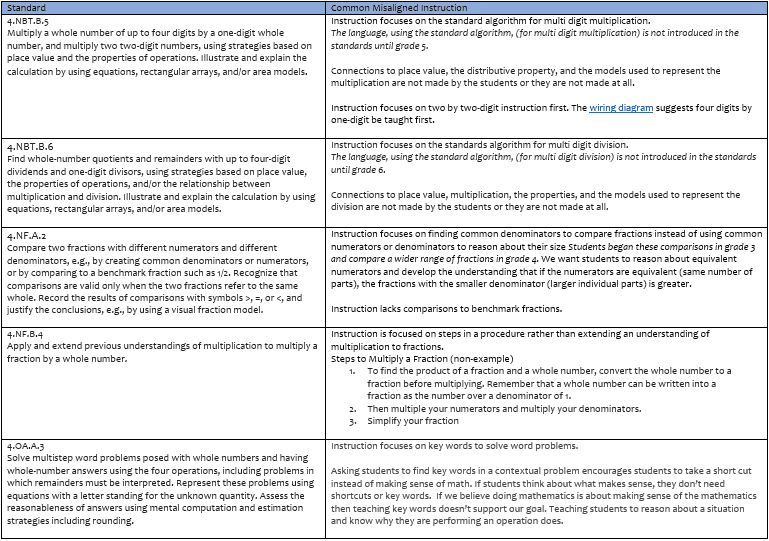
Do you mind sharing a link to the wiring diagram mentioned in the table at towards the beginning of the article? Since it’s an image, the hyperlink doesn’t actually work. Thank you!
Here’s the link to the wiring diagram! https://achievethecore.org/page/844/a-graph-of-the-content-standards
Thanks for your post. I can definitely understand how decomposing during division could be confusing.
These misundersoond standards posts are fantastic. By chance is there one for 5th grade?
Yes! It’s been drafted! Posting later this week!
I enjoyed the acronyms for division!
ALL Math Master Teachers in my parish needs to read this article. Wait!! HSE Math Master Teacher needs to read this article. As an educator, I try my best to keep up with research. I attended a summer program for educator. While attending, the professor talked about math misconceptions. She also provided us with books.
Well, I read the books and try my best to teach so my students would not have misconceptions about the standard I would teach. The MMT would enter my classroom sit for a while than jump up and say you are not teaching the student correctly. You are teaching them tricks.
I was teaching standard 4.NBT.B.5 using area model, distributive property, etc. My MMT stated that’s NOT the “Most Efficient” way to solve that problem.
Here comes the Principal. If your MMT said don’t teach it that way than you better not teach it that way. I said “okay” and continued teaching it using area model, distributive property, etc.
Well, I am no longer there because of the MMT, but I was not going to continue to teach our future her way.
Thanks for this article.
Thank you for reinforcing the need to UNDERSTAND the concept before the standard algorithm is taught. I find the hardest part is getting parents on board instead of jumping straight to the algorithm. Any advice? I’ve tried after school parent meetings and videos online. Still a struggle with argumentative parents.
Why isn’t there a place for both? Deeper understanding is a goal to strive for, but some students may not be ready for that. It is not all or nothing. There is a place for memorizing multiplication facts. There is also value in knowing the steps/process to long division. Maybe the concept is easier to understand after they know the process, not the other way around?
I just had this conversation about those standards with a colleague. I agree with a lot of things you’ve said. Being able to understand conceptual math is only going to go so far though…At some point, we have to take the bottle out of their month and let them eat solid food. Is the standard algorithm too much for multiplying multi-digit numbers in 4th grade? Probably so for most 4th graders. But you have some who have a sound enough understanding of place value to understand the standard algorithm. I was one of them. If the teacher had taught me the conceptual algorithm first, I wouldn’t have learned it at all. Tell me what to do first, then give me a backstory. Every child doesn’t learn the same way, and we can’t teach all children the same way.