In my last posts we explored the Most Misunderstood Elementary Mathematics Standards in Grades 3 and 4. I have loved the conversations I’ve engaged in with math educators and welcome more people to join in! I can be found on Twitter here: @few_rebecca or leave me a comment below!
In this post, we will dive into the most misunderstood elementary school standards in Grade 5. Again, this is not about judging our colleagues, but looking deeply at the practice of mathematics instruction in Grade 5 and learning more about the standards together.
| Standard | Common Misaligned Instruction |
| 5.NBT.A.1
Recognize that in a multi-digit number, a digit in one place represents 10 times as much as it represents in the place to its right and 1/10 of what it represents in the place to its left. |
Instruction is focused on multiplying by 10 or dividing by 10 to understand place value concepts without extending the students’ understanding of the base-ten system and the magnitude of digits in a number to the relationship between adjacent spaces. Also, opportunities are missed to develop an understanding of the relationships of digits in whole numbers to the relationship of decimal fractions. |
| 5.NBT.B.6
Find whole-number quotients of whole numbers with up to four-digit dividends and two-digit divisors, using strategies based on place value, the properties of operations, and/or the relationship between multiplication and division. Illustrate and explain the calculation by using equations, rectangular arrays, and/or area models. |
Instruction focuses on the standard algorithm for multi-digit division, and/or students learn a mnemonic to help them remember the steps to follow when dividing multi-digit numbers.
The language “using the standard algorithm” (for multi-digit division) is not introduced in the standards until grade 6. Connections to place value, the properties, and the models used to represent the division are not made by the students or they are not made at all. |
| 5.NBT.B.7
Add, subtract, multiply, and divide decimals to hundredths, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used. |
Instruction is focused on the steps to follow for completion rather than connections being made to what they already know about the base ten system. An example is provided below.
To multiply decimals:
Students aren’t applying what they know about place value and the area model from fourth grade as they begin to explore decimal multiplication. |
| 5.NF.B.4
Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction. |
Instruction is limited to steps in a procedure. Here’s an example:
To multiply proper fractions:
Absent from instruction is the use of concrete manipulatives or the drawing of models to demonstrate multiplication of proper fractions as taking a fraction of a fraction. (This supports the conceptual understanding and provides visual evidence that the product is less than the factors.) |
| 5.NF.B.5
Interpret multiplication of fractions as scaling. (resizing) |
Instruction focuses on the steps listed in the example above without an understanding of multiplying as scaling.
When students interpret multiplication as scaling, they compare the size of a product to the size of one factor on the basis of the size of the other factor, without performing the indicated multiplication and explaining why multiplying a given number by a fraction greater than 1 results in a product greater than the given number. (Or why multiplying a given number by a fraction less than 1 results in a product smaller than the given number.) |
| 5.NF.B.7 Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions. |
For division of whole numbers by unit fractions, instruction focuses on converting the whole to a fraction with a denominator of one and multiplying by the reciprocal of the divisor.
For division of a unit fraction by a whole number, instruction focuses on multiplying the denominator of the fraction and the whole number. When instruction is limited to procedures, students miss the opportunity to reason about how many groups of ½ are in 3 or what happens when a proper fraction is partitioned into more parts. |
How many times have we heard someone say, “When we multiply, the product is always larger” or, “When I divide, my answer is always smaller.” Probably several times during our tenure in education. When I hear these statements, my initial response is, “Really? Always?”
Making generalizations about mathematics that are inaccurate promote misunderstandings about important math concepts. These misconceptions can have unintended consequences for our students. I want to dig into two standards that disprove the statements above and challenge all of us to be more precise with our math language and communication.
The first one is 5.NF.B.4: Apply and extend previous understandings of multiplication to multiply a fraction or whole number by a fraction.
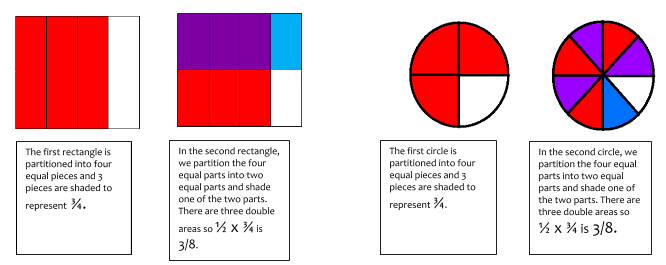
When I see a problem like ½ x ¾, I say to myself what is ½ of ¾? In the context of multiplication problems, “of” means to multiply. Thinking about it this way helps me visualize the problem and consider next steps.
Let’s take a look at ½ of ¾ using two area models:
The area model of fraction multiplication allows students to see that the multiplication of fractions results in a smaller product and helps to build fraction number sense, number sense related to fractions as opposed to whole numbers. This model can also be a visual for showing two fractions being close to one resulting in a product close to one.
The second standard we will explore together is 5.NF.B.7: Apply and extend previous understandings of division to divide unit fractions by whole numbers and whole numbers by unit fractions. The contextual problems below from Illustrative Mathematics allow students to apply what they know about mathematics to real-world situations.
Which of the following problems can be solved by finding 3 ÷ 1/2? How do you know?
- Shauna buys a three-foot-long sandwich for a party. She then cuts the sandwich into pieces, with each piece being 1/2 foot long. How many pieces does she get?
- Phil makes 3 quarts of soup for dinner. His family eats half of the soup for dinner. How many quarts of soup does Phil’s family eat for dinner?
- A pirate finds three pounds of gold. In order to protect his riches, he hides the gold in two treasure chests, with an equal amount of gold in each chest. How many pounds of gold are in each chest?
- Leo used half of a bag of flour to make bread. If he used 3 cups of flour, how many cups were in the bag to start?
The two problems we can solve by dividing 3 by ½ are “a” and “d.” For problem “a” we can reason about the answer without providing a model. Shauna has a sandwich that is 3 feet long. If she slices that sandwich into pieces so that each piece is ½ foot long and wants to know how many slices she would get, Shauna is really asking, “How many groups of 1/2 are in 3?” For problem “d” we can reason that if 3 cups of flour are half the bag, then 6 cups of flour were in the bag to start. This problem is asking “3 cups is 1/2 of what amount?” This Illustrative Mathematics task requires students to recognize both “number of groups unknown” (part a) and “group size unknown” (part d) division problems. It also addresses a common misconception that students have: they confuse dividing by 2 or multiplying by ½ with dividing by ½.
As I have said before, teaching elementary mathematics is anything but elementary! It requires intentional planning, a laser-like focus on mathematical concepts, and the ability to see math as a series of connected understandings. I firmly believe our collective goal is to support all students as they engage in rigorous mathematics. I hope my experiences in elementary school classrooms, both as a coach and a teacher, have supported your deepening understanding of the standards and, now that you know better, you will do better! Continue to #InstructUP!



















5.NBT.A.1 – I teach 7th grade. We just finished subtracting rational numbers. While teaching this unit, I gained a much greater understanding of the importance of this 5th grade standard. When relating fraction to decimals, it is easy to see that decimals are “lined-up” because their fractional equivalents have the same denominator. When subtracting mixed numbers that require borrowing, we do not borrow 1, but we borrow a whole. That whole maybe 4/4, 5/5, 6/6, ….
The understanding of place value is important in the development of students understanding of fractions, too.
Thank you for a fantastic article, Rebecca! Though I have plenty of room for improvement, I have been intentional in avoiding these mistakes with my 5th graders. It’s been quite the challenge un-teaching formerly thought absolutes, such as multiplication always results in a product larger than that of its factors. They were quite fixed in the beginning on the idea that taking “part of a part” must be subtraction because you’re “taking away.” It’s a challenge to get students to break expired rules, but it’s enjoyable to watch them struggle and finally see the math. Thanks again for sharing your wisdom.
Excellent article! I am having many of these issues with some of my freshman COLLEGE students. 5th grade teachers, please send us students who *understand* place value, multiplication, division, etc.!
😂😂😂
I’m new to 5th grade and your article was very eye-opening and informative. Thank you for sharing.
Hi, Rebecca! Your articles on the Grades 3-5 misunderstood standards are great. They are very succinct and hone in on key aspects of the shifts in instruction expected by the Core. I am sharing these resources with my network.
One piece of constructive feedback. You note that in the context of multiplication problems “of” means “to multiply.” I would caution against interpreting multiplication problems by means of identifying key words, although I understand that this isn’t exactly what you are doing. (You used this interpretation of a strict algebraic expression, which is, obviously, a bit different.) A natural line of questioning from students, leading to potential confusion, might be: “But why does ‘of’ mean to multiply? [I argue that this is not easy to explain, convincingly.] And does it always mean multiply, each time I see it in a multiplication problem? [No.]”
Instead, I would suggest concentrating on interpreting the circumstances of the problem, but holistically. If written symbolically, 1/2 x 3/4 is just a two-dimensional problem no different than any other multiplication problem (5 groups x 6 items per group, e.g.), where you are identifying 1/2 of a group in a set that has 3/4 of an item in each group and the product represents the collective quantity. Alternatively, thinking of a unitizing approach, if 2 x 3/4 = 3/4 + 3/4, and 1 x 3/4 = 3/4 (alone), then 1/2 x 3/4 must represent the number added to itself that will equal 3/4, or, ? + ? = 3/4.
A key words approach, or even one that alludes to a key words approach, often leads to misinterpretation by teachers and students. As one example, as part of a research project in which I participated, wherein asked students to “draw the fractions 1/2 and 3/4 on a number line.” We were surprised, but really shouldn’t have been, when they simply performed a computation and tried to add 1/2 and 3/4 (most unsuccessfully). They were familiar with the (false) idea that “and” means “add” and consequently misinterpreted the problem.
Thank you, again, for your great work and clear writing! You’ve fostered a lot of great conversations among our teachers!
Representing 10 x’s as much being the number to its left is a hard concept for students to grasp.
Yes! In my opinion, this is an abstract concept that the 10 year old mind is not developmentally ready to grasp yet.
I’m wondering how much of the “short-cutting” and teaching to find the answer rather than understand the process is related to standardized testing. With so many pressures on teachers to have high results on state tests, I can’t help but believe this is greatly impacting how teachers teach. And not necessarily in a positive way.
The highly debated and at times polarizing issue with long division, as well as “standard algorithm” is perplexing to me in general. Certainly, I am a HUGE advocate of number sense, estimation, area models, number bonds, composing and decomposing numbers in all sorts of ways, teaching children to be flexible with numbers, etc, however, I am also an advocate of making connections to the “procedures” through our conceptual understandings. We do this beautifully with area models to the partial products in the algorithm for multiplication. We see division in different forms and focus heavily on estimation with rounding, adjusting to compatible numbers, using factors and multiples, making the connection to multiplication clear as day, delving into the two MEANINGS of division (partitive and measurement), and so on. What I struggle with is why has “algorithm” become a “bad word” that will make it seem like I don’t understand the CCSSM!? I understand the fluency expectation for use of the standard algorithm is an expectation for the end of 6th grades, however, since it is such an involved procedure, shouldn’t students begin working with long division earlier grades, practice it 4-5 alongside other strategies for division and master it in 6th? Of course, I understand that long division is a procedure, however, it is a procedure based on place value that works by continuously unbundling and renaming the units in the dividend.
Let’s be CLEAR, I DO NOT teach a mnemonic, and I force my 5ths to use anything other than long division at various times throughout our units. So, please don’t confuse my honest query and need for professional discussion as anything other than that.
I also read this very beautiful article in a mathematics course I took as an undergrad. It has stayed with me. https://math.berkeley.edu/~wu/wu1999.pdf