Over the past five years I have had the privilege of visiting many mathematics classrooms, over 1,000 and counting. People who know me well know I am either talking about mathematics instruction, reading about mathematics instruction, or planning for mathematics instruction. I define myself as an instructional nerd! One of the many perks of my classroom visits is the opportunity to provide feedback to teachers, instructional coaches, and administrators. I use the Instructional Practice Guide for Coaching as my lens for lesson observation and feedback. You can learn more about the coaching tool here.
During my visits, I definitely have noticed some trends in instruction. There are some standards, regardless of the teacher, the school, or the district that seem to be commonly misunderstood. Somehow the intent of these standards is lost during instruction. I do not believe this is ever done intentionally, but could be a byproduct of many factors. Maybe it is because old standards are still lingering in the current curriculum; maybe lessons and/or materials have been recycled or repurposed from before the Common Core State Standards; or maybe there is a lack of understanding of what the standard actually means. Regardless of the reason, I would like us to learn and grow our brains together! I hope through this series of posts, a broader network of math educators will be better equipped to plan for and implement standards-based instruction.
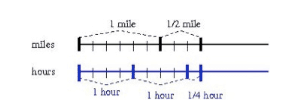
I would like to look more in-depth at two of these standards, starting with my favorite Grade 6 math standard, 6.NS.A.1. It is such a beautiful standard if understood and instructed for understanding! Let’s look at this task from Illustrative Mathematics.
Each of the solution paths shown above relies on visual models over the algorithm for division of a fraction by a fraction. No need for “Keep, Change, Flip” as students are making sense of fraction division through context using models! There are problems where models do not make sense. I mean, who wants to draw a model for 5 2/5 ÷ 3/7? So, if your learning goal is focused on using visual models, be strategic with the number choice used in your problems!
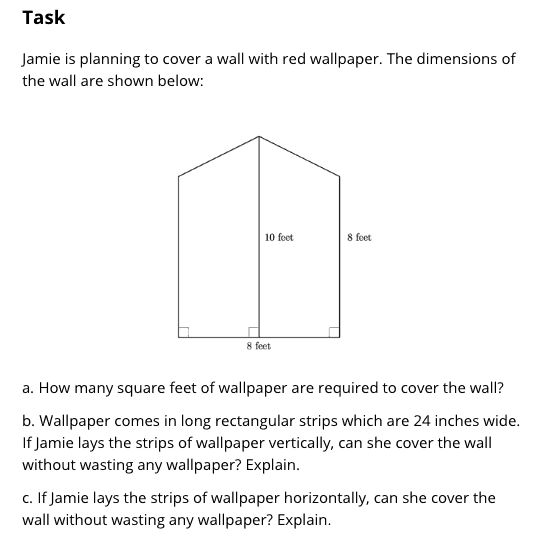
The next standard of interest is 6.G.A.1. The intent of this standard is to have students composing and decomposing figures in order to find the area of composite figures. These Illustrative Mathematics and EngageNY tasks are examples of the type of tasks that students should be engaging in to meet the intent of this standard. Both problems expect students to decompose the given figure into rectangles and/or triangles in order to find the area of the shape. There is no need to require students memorize the area of a trapezoid! They should decompose it into shapes for which they know how to find the area!
The suggestions given here are just a start to figuring out this very challenging profession of teaching students mathematics. I hope my experiences in many middle school classrooms will help grow your brain around these standards and now that you know better, you will do better in ensuring each student learns math at a high level. Next month, Most Misunderstood Middle School Mathematics Standards in Grade 7. Stay tuned and #InstructUP!





















Hello this was very helpful. Can you elaborate more on the ratio one. The first one you listed as a “misaligned instruction” Thank you.
Yes, please, I was thinking the same thing, and as a coach I would appreciate more clarification on that first point. Great article!
I would like your thoughts on the ratio one.
I understand that the ratio focus should not be on the three ways to write a ratio, but I don’t think we can stop using that one altogether. Our students need to know what ratios look like written in all three ways. While this isn’t the focus of the standard, it is still relevant information.
Hello! First of all, thank you so much for reading this blog. I am glad so many people have found this information I have collected over the last couple of years useful. To clarify the ratio misaligned instruction, you are correct, students do need to be able to describe quantities using ratio language. The instruction I am speaking about is limited to just creating a foldable on the three ways to write a ratio and then completing a worksheet on the topic. The reasoning and understanding gets lost. The second point I am trying to make is the confusion caused for students when writing a part part ratio using fraction notation. So 6/2 describing boys to girls and the quotient of 6/2. It does have a value of 3 (or 3/1). So “let’s stop using this one” might be a bit strong. Maybe be more aware of the confusion caused when using this representation of a ratio for students when it is a part-part relationship? As I stated in the blog, I am always willing to learn together! Let me know your thoughts!
I totally agree that fraction notation should not be used for part:part ratios – if you have 2 blue tiles and 3 red tiles, then writing the ratio as 2/3 for anything is very confusing. That said, do you think fraction notation can/should still be used for part:whole ratios? I found that, when we worked with ratios and different models for ratios, and that saw that “2 out of 5 tiles were blue so 4 out of 10 tiles would be blue” acted the same way as “⅖=4/10”, it helped give a concrete understanding of equivalent fractions for those who still needed to solidify that understanding. In other words, by using fraction notation, kids were able to deepen or solidify their understanding of fractions, and build procedural fluency for equivalent fractions while bridging to an understanding of ratios. I’m wondering if this was a fluke (this was my 24th year teaching but first in sixth grade), or if this will have unintended consequences down the road.
The problem here is the use of symbol…. “/” In the English lesson “/” means something completely different…. eg can/should…. And then in the math class we tell them it means to divide… 2 divided by 3…. but then we confuse the students by saying it also means it is a ratio… which is actually correct but…. The real takeaway is to Stop thinking like a mathematician and Start thinking like a student… Yes, the world is round… but is the student thinking round like a ball or round like a plate???
My team and I struggle with the percents standard every year. We all teach it very differently and when we rotate kids for target time (ability based grouping), the kids get more confused. I think we teachers are confused on this one. Could you elaborate on what the misconception is and explain a little more? Thank you.
This is a great article, thank you. I’d also like more clarification on 6.RP.A.1- like someone else already said, I think that students need to be able to identify the different forms of writing ratios. I think that is not just knowing that 6:2 represents a ratio, but also understanding the meaning of the values or what they stand for. Can’t stop instruction on that, but should not be the main focus.
I believe when writing ratios in fraction form, it is important to include labels so that students understand what type of comparison we have (part to whole or part to part).
We need a twitter chat so we can share ideas, and get clarification in real-time, ok at least something closer to real-time.
Great idea, Marcia! @achievethecore will host one in 2020. Stay tuned!
Hi Marcia, Thanks for this idea! We will be having a Twitter chat on this blog series on Tuesday, February 25th at 7 p.m. ET. We hope you’ll join! Follow along using #coreadvocates or follow us @achievethecore.
I would love to obtain a shareable link to the above article. Is there a way to do this?
Hi Pamela:
You can share this link below:
https://achievethecore.org/aligned/misunderstood-middle-school-mathematics-standards-grade-6/
Take care.
Write ratios three ways? Still too procedural. A nother bit of so-called math that NO ONE ever uses except in an elementary schopl. Draw a diagram for the first problem? Ok, but a waste of time for the student who writes (3/2 mi)/(2/3 mi/hr) = 9/4 hr = 2:15. And what happened to the units, which are the real key to getting this problem right? If you have miles, and miles per hour, it’s pretty obvious that you have to divide to convert miles to hours.
Don’t torture the kids who get it by forcing them to explain it to a teacher who doesn’t.