During the May 2017 Core Advocates convening, I attended a session with Astrid Fossum and Chrissy Allison, where we discussed how to address unfinished learning while also engaging students in grade-level math instruction. Astrid and Chrissy put together a list of Recommendations for Targeted Math Support and Interventions, which you can read about here.

One of these recommendations has been on my mind quite a bit lately:

We’ve all heard the old adage: “If at first you don’t succeed, try, try again.” And as teachers we are masters at trying again, right? Research and our own experiences have shown us that students need multiple exposures and opportunities to make sense of math concepts and explore ideas, but planning for and engaging students in the “right” experiences is key to meaningful learning.

Let’s think about fact fluency. In my current role as a Mathematics Specialist, I design and facilitate professional learning for PreK-5 elementary teachers and administrators in schools and districts across the state of Wisconsin. Fact fluency is a topic that comes up often as I work with educators—more specifically, teachers want to know what to do with students who just don’t know all of their facts. This is a frustration I know quite well, as I felt it often when I was in the classroom teaching grades 4-5. The curriculum materials my school used didn’t provide me with any support in this area, and I wasn’t lucky enough to have an instructional coach or content specialist in the building to collaborate with, so I did what I thought was best at the time.

My plan of attack ten years ago was to do weekly fact drills and play fluency games a few times each week, with the hope that students’ knowledge and recall of multiplication and division facts would improve. My misstep was continuing to provide more of the same kinds of practice activities students had already done in previous grades and thinking that would help my students know their facts better. Why did I think that doing more of the same would lead to different results? The kids who were already secure with their facts flew through the fact drills and earned the fun incentives, while a significant fraction of my class stalled in mastering anything beyond their five facts.

A better way to address my students’ unfinished learning would have been to use the 3-step approach Understand-Diagnose-Take Action, which you can read about here. I understood that many of my students didn’t yet know all of their facts, which made it more difficult for them to engage with grade-level content. If I had taken time to diagnose, I would’ve seen that students didn’t have strategies to figure out the facts they didn’t know, which often resulted in random guessing or painful silence.

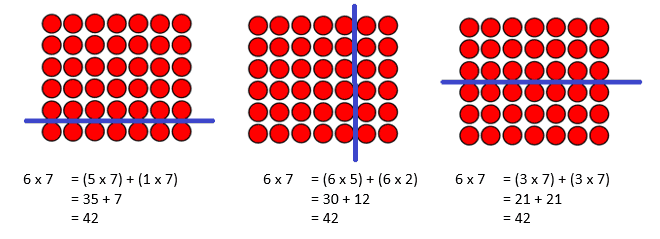
A more effective way to take action would be to re-engage students in learning their facts using tools and models, to help them develop thinking strategies for the facts they didn’t know—often the 6s, 7s, 8s, and 9s. For example, when thinking about a tough fact like 6 x 7, we could model the fact with an array, and then discuss ways to split the array so we could use facts we know to help find the product. This “new” learning experience offers an opportunity to discuss and explore how and why the distributive property works, and it provides students with a strategy they might use to think about other facts they are not solid with yet.

Another area of unfinished learning where teachers might re-engage students with new experiences is place value. One of the big ideas around place value is the understanding that numbers can be decomposed in different ways (understand). If students are struggling with place value concepts, the disconnect may be rooted in an incomplete understanding of part-whole relationships and the structure and flexibility of the base-ten number system (diagnose). Rather than giving students endless practice sheets where they simply identify the number of hundreds, tens, and/or ones in given numbers, teachers might consider engaging students in activities where they can dig into place value concepts at a more conceptual level, such as the “Three Composing/Decomposing Problems” task from IM (take action). This task supports students in considering how numbers can be decomposed in different ways, through concrete representations and opportunities to talk about their thinking and build shared understanding.

I wish I had engaged in this kind of instructional thinking when I was back in the classroom working with my intermediate students. There’s so much more that I could have done with my fourth and fifth graders to build their conceptual understanding of mathematical concepts, boost their confidence, and set them up for success. Now that I know better, I work to help other teachers do better. How will you do better for your students? Tweet @achievethecore and @mathinst_Kristi (that’s me!) sharing what you do or plan to do in the future!”