When was the last time you had to engage in an activity that required you to “unpack” mathematics standards? Perhaps you spent hours on the task, circling verbs and underlining nouns, to end up feeling only marginally better prepared to teach the standards. In mathematics, this way of digging into standards can too easily result in unintentionally separating ideas that were intended to stay together as it ignores some of the higher-level organizing structures that reflect the coherence of the discipline. For more on this, we recommend visiting or revisiting The Structure is the Standards. Additionally, though, unpacking also risks overlooking or reducing the intended complexity of the mathematics students should be learning. To increase complexity, we often need to look at how mathematical ideas from different standards are connected or consider how to integrate content standards with the Standards for Mathematical Practice.
What is cognitive complexity and how do we think about it in a way that helps us deepen the mathematics students are learning? Let’s start with a different approach to unpacking standards where we approach the work first through the domain, instead of through an individual standard, using grade 3 fractions as an example. First, based on the overall structure of the standards, we see that students’ real work on fractions begins in grade 3 when the domain “Number and Operations—Fractions” first appears. Next, we notice just a single cluster: “Develop understanding of fractions as numbers.” This signals that the heart of the work with fractions in grade 3 should be on building conceptual understanding – not on application and not on procedural skill and fluency. The domain and cluster tell us a lot about the full expectations of the standards.
Next, as we read several standards, we see some are definitional, while others require deeper levels of understanding. We also need to attend to concepts that cut across these standards that should also be integrated. As an example, let’s look at a couple of assessment items that claim to assess these standards. As we do, we will unpack the mathematical complexity of each and then apply A Framework to Evaluate Cognitive Complexity in Mathematics Assessments, which is a tool that allows us to formalize the complexity analysis to better understand the mathematical demands of each item.
Item #1

Source: https://achievethecore.org/content/upload/SAP_Mini-Assessment_Grade-3.pdf
Item #2

Source: https://achievethecore.org/content/upload/SAP_Mini-Assessment_Grade-3.pdf
In the standards, a fraction a/b can be located on a number line by defining the interval from 0 to 1 as the whole and partitioning this distance into b equal parts where each interval is then 1/b. So in Item #1, a student needs to understand this definition of a fraction and apply it to recognize that the whole is partitioned into eighths, and the star is located on the third one, or at 3/8.
Item #2, on the other hand, can be approached in a variety of different ways. First, students must get over the initial shock that the fraction 1/3 is on the second mark and not the first mark. Then, they can either use that 1/3 distance to locate 2/3, 3/3, and so on, or they can start by generating an equivalent fraction of 2/6 and using this to locate other fractions. In either case, students must apply knowledge from multiple standards within the domain to correctly place both of the fractions given.
Getting back to that complexity framework…one of the major differences between this new framework and prior frameworks (e.g., Depth of Knowledge) is that it is grounded in one of the three Shifts required by college- and career-ready standards, which is that we balance the mathematics students are learning on conceptual understanding, procedural skill and fluency, and application. Rather than a single complexity rating for a particular problem, the framework allows us to examine and code the specific and varying sources of mathematical complexity. Table 1 provides descriptors that allow us to evaluate assessment items according to the three sources of mathematical complexity. The middle row, which shows conceptual complexity, is the one that we can use to evaluate Items #1 and #2 shown earlier.
Table 1. Levels of Complexity 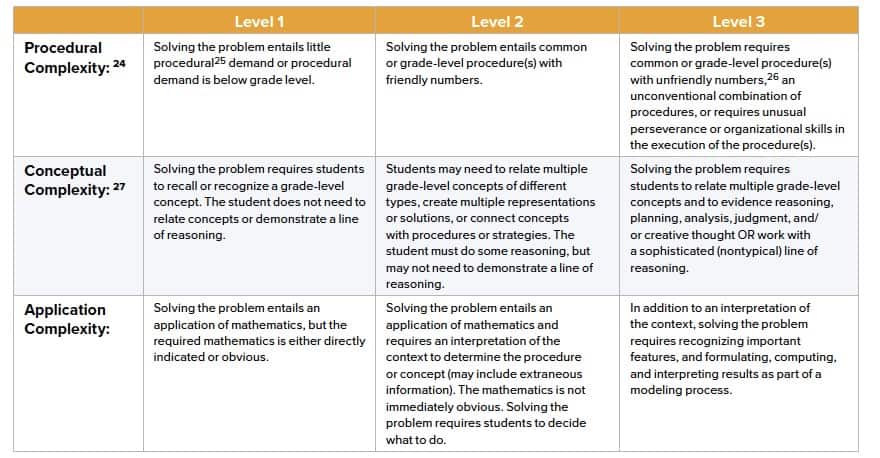
In Item #1, students need to recognize the grade-level concept of a fraction, but they do not need to relate concepts or demonstrate a line of reasoning, so this is a fairly typical example of an item at Conceptual Complexity Level 1. In Item #2, students do need to relate multiple grade-level concepts, raising that problem to Conceptual Complexity Level 2. It is important to note that a Level 1 item doesn’t signal that it is a bad question; it could just mean that it is measuring one of the more foundational aspects of the standards. The standards require a range of complexity, so this is what we should be seeking in our work with students.
The next time you are asked to “unpack” standards, we encourage you to take a look at the framework and use it along with the higher-level organizing structures of the standards to ensure that the exercise of unpacking includes opportunities to make connections across mathematical ideas. Although the framework was specifically designed for use in evaluating assessment items for cognitive complexity, it can also provide a useful lens for us to think about whether we are reaching the full depth of the math standards.

















